Étiquette : Apprentissage efficace

Publié le

Apprendre les mathématiques autrement : ce que la recherche nous enseigne

Pendant longtemps, apprendre les mathématiques a été synonyme de répétition, de formules à mémoriser et de contrôles stressants. Pour certains élèves, ça fonctionnait. Pour beaucoup d’autres, c’était le début d’un décrochage durable, parfois accompagné d’une véritable angoisse face aux maths.

Depuis plusieurs années, la recherche en didactique des mathématiques explore d’autres voies. Pas pour “simplifier” les maths ou les rendre moins exigeantes — mais pour les rendre plus compréhensibles, plus justes et plus accessibles à tous les élèves.

Dans cet article, je te propose de faire le point sur ce que ces recherches nous apprennent, et surtout sur ce que cela change concrètement dans la façon d’apprendre (et d’enseigner) les maths.

Pourquoi repenser l’apprentissage des maths aujourd’hui ?

Les constats sont largement partagés :

• une partie importante des élèves développe une relation anxieuse aux mathématiques,

• beaucoup pensent très tôt qu’ils ou elles ne sont “pas faits pour ça”,

• les inégalités scolaires se creusent rapidement autour de cette discipline.

Or, les mathématiques restent une matière centrale : elles structurent la pensée logique, la capacité à raisonner, à modéliser le réel, à prendre du recul. Le problème n’est donc pas les maths en elles-mêmes, mais la manière dont elles sont souvent abordées.

La recherche montre que lorsque les élèves comprennent ce qu’ils font, pourquoi ils le font et comment ils peuvent chercher, leur rapport aux maths change profondément. C’est ce qu’explique cet article de The Conversation version française.

Apprendre sans que l’enseignant donne la solution : les situations adidactiques

Un concept clé de la recherche s’appelle la situation adidactique. Derrière ce terme un peu technique se cache une idée simple : placer l’élève dans une situation où il peut chercher, tester, se tromper, ajuster… sans que la solution soit donnée immédiatement par l’enseignant.

Concrètement, cela peut prendre la forme :

• d’un jeu mathématique,

• d’un défi logique,

• d’un problème ouvert avec plusieurs stratégies possibles,

• d’une situation proche du réel.

L’élève n’applique pas une recette : il construit activement le raisonnement. Et c’est précisément cette phase de recherche qui permet un apprentissage durable.

Donner du sens : contextualiser les mathématiques

Un levier majeur identifié par la recherche consiste à ancrer les mathématiques dans des situations compréhensibles et concrètes.

Lorsqu’un élève travaille sur un partage équitable, une optimisation, une comparaison de quantités ou une évolution dans le temps, il comprend pourquoi les mathématiques sont utiles. Les notions ne sont plus abstraites par défaut : elles deviennent des outils pour penser le monde.

Cela ne veut pas dire abandonner les notions formelles, mais les introduire au bon moment, quand elles répondent à un besoin identifié par l’élève.

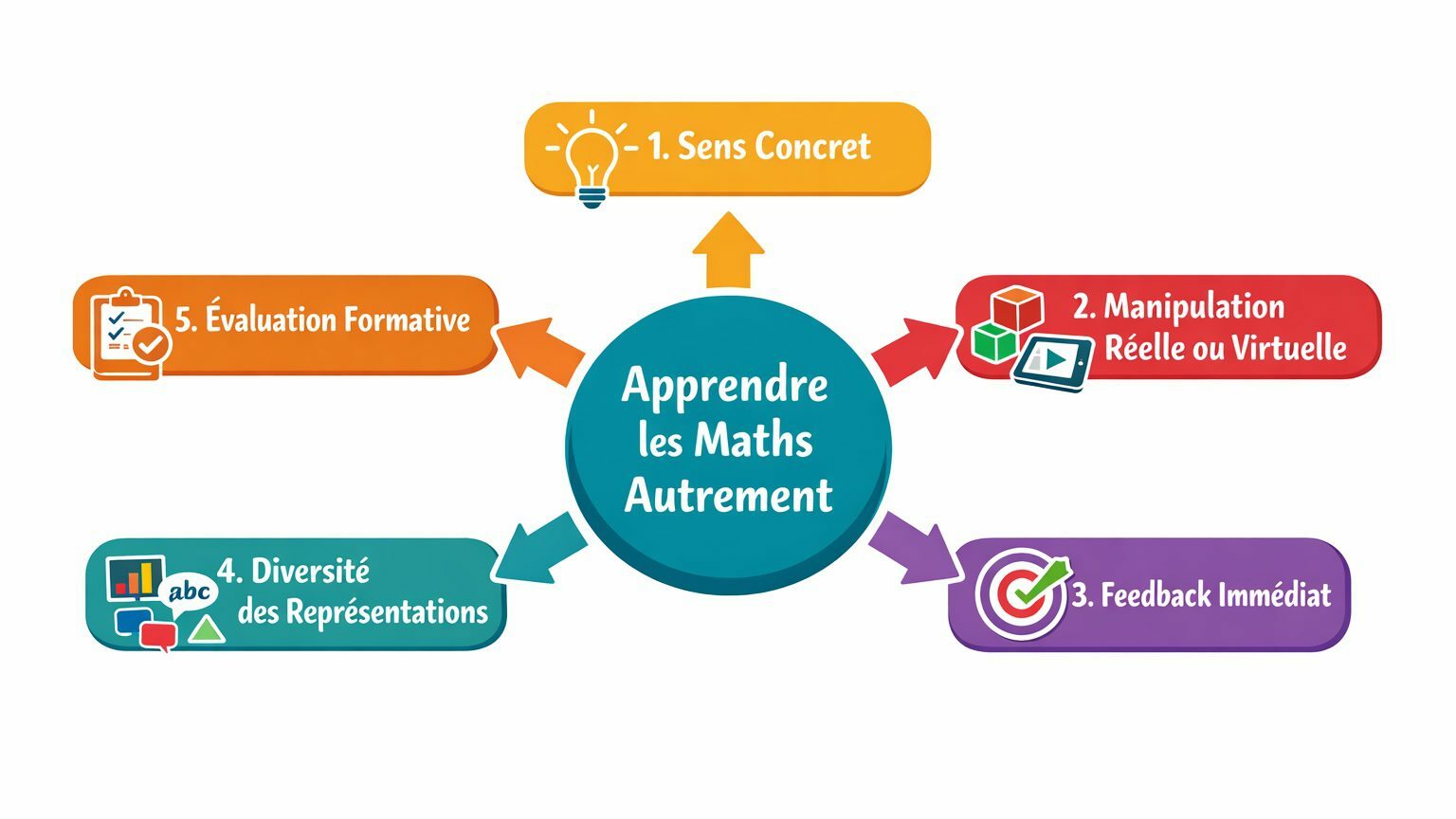
Manipuler, visualiser, représenter autrement

Les recherches montrent également l’importance de diversifier les représentations. Un même concept mathématique peut être exploré :

• avec des objets à manipuler,

• par un dessin ou un schéma,

• à l’aide d’un graphique,

• via un outil numérique interactif,

• par une mise en mots orale ou écrite.

Ces allers-retours entre représentations permettent aux élèves de mieux comprendre les liens entre les notions ; ils apprennent aussi à dépasser les blocages liés à une seule forme d’explication et à développer une vraie flexibilité mentale.

Les outils numériques bien utilisés (manipulatifs virtuels, visualisations dynamiques) peuvent ici être de précieux alliés, à condition qu’ils servent la compréhension — et non la distraction.

Tout le monde peut réussir en maths. À condition de bien s'y prendre.
Tout le monde peut réussir en maths. À condition de bien s’y prendre.

Évaluer autrement pour faire progresser

L’évaluation est presque toujours perçue comme une sanction. La recherche propose un changement de regard : évaluer pour apprendre, pas seulement pour classer.

Cela passe par des retours réguliers et précis, des erreurs analysées comme des étapes normales du raisonnement, des évaluations intégrées au travail quotidien et des moments de verbalisation : comment as-tu fait ? pourquoi ?

Cette approche renforce la confiance des élèves et leur capacité à s’auto-corriger, une compétence essentielle bien au-delà des mathématiques.

Le rôle clé de l’enseignant… et de l’accompagnement

Ces approches ne reposent pas sur une méthode miracle.

Elles demandent une posture d’accompagnement, une écoute attentive des raisonnements des élèves et donc une formation continue pour les enseignants.

Changer la manière d’enseigner les maths, ce n’est pas tout bouleverser du jour au lendemain. C’est ajuster progressivement, tester, observer, affiner.

C’est aussi ce que je fais au quotidien dans mon accompagnement : partir de là où en est l’élève, de ce qu’il comprend déjà — même confusément — pour l’aider à structurer sa pensée.

Quelques exemples concrets à mettre en pratique

Voici quelques pistes simples, inspirées des travaux de recherche :

• proposer un problème avec plusieurs stratégies possibles,

• demander à l’élève d’expliquer comment il a cherché, même si le résultat est faux,

• utiliser des erreurs “classiques” comme point de départ d’une discussion,

• alterner calcul, dessin, verbalisation, manipulation,

• valoriser le raisonnement autant que le résultat.

Ces petites choses, répétées dans le temps, transforment profondément la relation aux mathématiques.

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Réconcilier les élèves avec les maths, durablement

Les recherches sont claires : les élèves apprennent mieux les mathématiques lorsqu’ils sont acteurs de leur apprentissage, lorsqu’ils comprennent le sens de ce qu’ils font, et lorsqu’ils ont le droit de chercher.

Apprendre les maths autrement, ce n’est pas les rendre plus faciles. C’est les rendre plus intelligibles, plus humaines et plus justes.

Et c’est aussi une excellente nouvelle : cela signifie que chacun peut progresser, avec le bon accompagnement.

Et toi ?

As-tu déjà vécu un déclic en maths grâce à une autre manière d’apprendre ?

N’hésite pas à partager ton expérience ou à me contacter si tu souhaites en discuter.

Publié le

La répétition espacée pour mémoriser les maths ?

Temps de lecture 7 minutes

Parlons aujourd’hui d’une méthode aussi efficace qu’élégante : la répétition espacée. Vous savez, cette technique qui consiste à réviser intelligemment au lieu de rester collé à son cahier jusqu’à ce que les formules vous dansent devant les yeux comme un écran de veille des années 2000.

Je vais vous montrer comment appliquer cette méthode à l’apprentissage des maths, que vous soyez collégien ou lycéen. Alors, c’est parti pour une plongée dans l’art de ne pas oublier ce qu’on vient d’apprendre !

La répétition espacée : qu’est-ce que c’est ?

Apprendre les mathématiques peut souvent ressembler à une montagne à gravir, avec des notions qui semblent disparaître dès qu’on tourne la page. La répétition espacée est une méthode idéale pour ancrer durablement ces connaissances et progresser de manière efficace. Voici comment elle fonctionne :

La répétition espacée, c’est un peu comme arroser une plante : vous ne videz pas tout votre arrosoir d’un coup (comprenez : réviser tout la veille du contrôle), mais vous donnez juste ce qu’il faut, au bon moment, pour que la plante (votre cerveau) puisse pousser tranquillement.

En clair, il s’agit de réviser les notions à des intervalles de plus en plus longs. Pourquoi ? Parce que c’est ainsi que fonctionne notre mémoire. La première fois que vous apprenez quelque chose, votre cerveau l’oublie rapidement. Mais si vous le revoyez avant que l’oubli soit complet, il le retient mieux. Et ainsi de suite, jusqu’à ce que cela devienne un souvenir durable. Merci Ebbinghaus et sa fameuse courbe de l’oubli !

Supposons que vous ayez un cours aujourd'hui. C'est la pastille rouge. Supposons encore que vous avez écouté et que vous avez l'impression d'avoir tout compris. Vouis êtes sûr de retenir sans effort. Ben non. Regardez la courbe rouge. C'est la courbe de l'oubli. Demain vous ne saurez plius que 50% du cours et presque plus rien dans une dizaine de jours.<br/>Faites une révision intégrale demain (R1) pour remettre votre mémoire au niveau de ce que vous saviez pendant le cours. Puis une autre dans trois jours (R2) et une autre dans 6 jours et peut-être même une dernière dans 12 jours.<br/>Là, oui, vous aurez tout retenu et pour ttrès longtemps. Votre mémoir aura suivi la courbe verte, celle de la mémorisation, du savoir. La répétition espacée pour mémoriser les maths
Supposons que vous ayez un cours aujourd’hui. C’est la pastille rouge. Supposons encore que vous avez écouté et que vous avez l’impression d’avoir tout compris. Vous êtes sûr de retenir sans effort. Ben non. Regardez la courbe rouge. C’est la courbe de l’oubli. Demain vous ne saurez plus que 50% du cours et presque plus rien dans une dizaine de jours.
Faites une révision intégrale demain (R1) pour remettre votre mémoire au niveau de ce que vous saviez pendant le cours. Puis une autre dans trois jours (R2) et une autre dans 6 jours et peut-être même une dernière dans 12 jours.
Là, oui, vous aurez tout retenu et pour très longtemps. Votre mémoire aura suivi la courbe verte, celle de la mémorisation, du savoir.

En termes simples, c’est une technique qui vous aide à « muscler » votre mémoire. Et le meilleur, c’est que cette méthode fonctionne pour tout type d’apprentissage, mais elle est particulièrement puissante en maths.

Pourquoi la répétition espacée est-elle si efficace pour les maths ?

Les maths… Cette belle discipline où tout s’emboîte, mais où tout peut aussi s’effondrer si vous oubliez une petite formule au passage. La répétition espacée est particulièrement utile en maths parce que :

  1. C’est cumulatif : Les notions de maths s’accumulent comme des briques. Si vous avez oublié une brique de base (exemple : Pythagore), vous aurez du mal à bâtir un mur solide (exemple : trigonométrie).
  2. Les maths demandent de la pratique régulière : Il ne suffit pas de lire un théorème pour le comprendre. Il faut le manipuler, encore et encore.
  3. Cela aide à lutter contre la surcharge cognitive : Revisiter régulièrement les notions permet d’éviter d’“empiler” trop de nouvelles informations sans consolider les anciennes.
  4. Elle renforce la compréhension active : La répétition espacée, combinée à des exercices variés, aide à passer de la simple mémorisation à une compréhension approfondie. Vous ne vous contentez pas de réciter une formule, vous comprenez pourquoi elle fonctionne.

En somme, cette méthode s’adapte parfaitement à la nature logique et progressive des mathématiques.

Comment pratiquer la répétition espacée en maths ?

1. Identifiez ce qui doit être révisé

La première étape, c’est de savoir quoi réviser. Voici quelques pistes :

  • Les formules : Aire d’un cercle, théorème de Thalès, trigonométrie, etc.
  • Les démonstrations types : Exemple : Montrer que la somme des angles d’un triangle fait 180°.
  • Les méthodes : Résoudre une équation du second degré, calculer une limite, tracer un graphique.

Pour chaque chapitre, faites une liste de ces éléments. Par exemple, dans un chapitre sur les fonctions, notez les notions essentielles : équations, variations, courbes et tangentes.

2. Organisez vos révisions

Adoptez un calendrier simple et progressif, basé sur les principes de la courbe de l’oubli : lorsque vous révisez une notion juste avant de l’oublier complètement, vous en renforcez la mémorisation de manière optimale. Ces intervalles progressifs permettent de ralentir le déclin naturel de la mémoire tout en consolidant les connaissances.

  • Jour 1 : Vous apprenez la notion.
  • Jour 2 : Vous la revoyez rapidement.
  • Jour 4 : Vous la revalidez avec un exercice.
  • Jour 8 : Vous la revoyez encore une fois.
  • Jour 15 : Vous testez votre maîtrise.

C’est flexible : adaptez les intervalles à votre rythme et à la difficulté des notions.

Alimentée à intervales réguliers, la mémoire peut libérer toute la puissance de ses super-pouvoirs.

3. Créez des fiches efficaces

Les fiches sont un outil puissant. Voici comment les organiser :

  • Fiches pour les formules : Par exemple, une fiche pourrait contenir au recto la formule d’un cylindre (V = πr²h) accompagnée d’une explication claire de chaque terme, et au verso, un exemple chiffré : “Calculez le volume d’un cylindre de rayon 3 cm et de hauteur 5 cm”.
  • Fiches pour les démonstrations : Listez les étapes clés d’une démonstration. Par exemple, pour le théorème de Thalès, incluez un schéma annoté sur le recto et les étapes de la preuve au verso.
  • Fiches pour les erreurs courantes : Notez une erreur typique que vous faites, par exemple “Oublier de multiplier par le coefficient directeur”, et ajoutez au verso la réponse corrigée avec une explication de la solution.

4. Utilisez des outils numériques

Les applications comme Anki ou Quizlet sont parfaites pour appliquer la répétition espacée. Vous pouvez créer des cartes interactives :

  • Question : Quelle est la dérivée de sin(x) ?
  • Réponse : cos(x).

Ces outils permettent de suivre votre progression et de vous concentrer sur vos points faibles.

5. Adaptez les exercices aux révisions

Pour chaque révision, variez les types d’exercices :

  • Au début : Des exercices simples pour fixer les bases.
  • Progressivement : Des problèmes plus complexes pour renforcer votre maîtrise.

Exemple concret pour les collégiens et les lycéens

Prenons l’exemple des formules de trigonométrie (sinus, cosinus, tangente). Voici comment structurer vos révisions :

  1. Créez des fiches :
  • Une fiche avec les valeurs exactes pour 0°, 30°, 45°, 60° et 90°.
  • Une fiche avec les identités trigonométriques principales (cos²(x) + sin²(x) = 1).
  1. Apprenez par étapes :
  • Jour 1 : Répétez les valeurs exactes à l’oral ou écrivez-les.
  • Jour 4 : Faites un exercice simple où vous devez utiliser ces valeurs.
  • Jour 8 : Essayez un exercice plus complexe où vous combinez plusieurs notions.
  1. Testez-vous :
  • Créez un quiz rapide sur ces formules.
  • Réalisez des exercices corrigés pour vérifier votre compréhension.

Les erreurs à éviter

Parce que, oui, même la meilleure méthode peut être mal appliquée :

  1. Ne pas respecter les intervalles : Si vous laissez passer trop de temps entre deux révisions, vous oublierez tout. Inversement, répéter trop souvent peut être contre-productif.
  2. Se contenter de lire : La révision passive (“Je lis ma fiche”) est bien moins efficace que la révision active (“Je résous un exercice”).
  3. Vouloir tout faire d’un coup : Priorisez les notions essentielles.

Compléments et approfondissements

Associer la répétition espacée à d’autres techniques

  • Pratique active : Combinez la répétition avec des exercices variés.
  • Mind maps : Créez des cartes mentales pour visualiser les liens entre différentes notions.
  • Gamification : Transformez vos révisions en jeu (score, défis).
Cette carte mentale, par exemple, reprend toutes les notions à savoir sur les fonctions. La répétition espacée pour mémoriser les maths
Cette carte mentale, par exemple, reprend toutes les notions à savoir sur les fonctions.

Un plan sur l’année scolaire

  • Avant les contrôles : Revoir les notions à intervalles réguliers.
  • Pendant les vacances : Consolider les bases et anticiper les prochains chapitres.
  • Préparation aux examens : Reprendre systématiquement les notions clés depuis le début de l’année.

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Un dernier mot

La répétition espacée, c’est un peu comme l’entretien d’une voiture : il faut y aller régulièrement pour éviter les pannes (ou les trous de mémoire en plein contrôle !). Alors, prenez le temps de structurer vos révisions, soyez patients et, surtout, amusez-vous à constater vos progrès. Vous verrez, les maths deviendront moins intimidantes et bien plus accessibles.

Et si vous avez des questions ou des retours d’expérience, partagez-les dans les commentaires. Je suis là pour vous aider à développer vos super-pouvoirs mathématiques !

Quelques ressources gratuites

Pour vous donner un coup de main et pour vous montrer qu’on peut facilement s’organiser pour être plus efficace dans ses révisions, je vous ai préparé trois petits modèles qui pourraient vous être utiles. Vous êtes libres de les télécharger, de vous en inspirer, de les modifier mais surtout… de vous en servir !