Mois : décembre 2024

Publié le

Le concept de “Growth Mindset” : adopter une mentalité de croissance

growth-mindset-apprentissage-maths
temps de lecture 7 minutes

“Becoming is better than being.”
Traduction : « Devenir est mieux qu’être. »

Carol Dweck

Imaginez un élève devant une équation. Elle semble imbattable, comme un boss final dans un jeu vidéo. Deux réactions possibles : “Je ne suis pas fait pour ça” ou “C’est difficile, mais je vais y arriver”. À votre avis, laquelle fera avancer cet élève ?

C’est ici qu’entre en scène le concept de Growth Mindset, ou mentalité d’évolution. Inventé par la psychologue américaine Carol Dweck, ce concept pourrait bien révolutionner votre façon de voir l’apprentissage… et même les maths ! Oui, oui, les maths !

Dans cet article, on plonge dans cet état d’esprit transformateur, ce switch mental cher à la PNL (Programmation Neuro-Linghuistique) de Richard Brandler. On découvre pourquoi il est crucial pour progresser et surtout, comment l’appliquer dans l’univers des chiffres et des équations. Vous allez voir, c’est bien plus simple (et fascinant) qu’il n’y paraît.

Qu’est-ce que le Growth Mindset ? Une histoire de croyances

Le Growth Mindset, ou mentalité de croissance, est un concept développé par Carol Dweck, professeure à l’université de Stanford, dans les années 1980. Elle a passé des années à étudier pourquoi certaines personnes réussissent mieux que d’autres dans des situations identiques. Le résultat ? Tout se joue dans la manière dont nous percevons nos capacités.

Deux mentalités s’opposent :

  • La mentalité rigide : croire que nos capacités sont innées, gravées dans le marbre (“Je suis mauvais en maths”, point barre).
  • La mentalité de croissance : croire que nos capacités peuvent se développer avec de l’effort et des stratégies adaptées (“Je ne comprends pas encore, mais je vais progresser”).

Dweck explique que la mentalité rigide nous enferme dans une peur de l’échec et de la remise en question. Alors que la mentalité de croissance nous pousse à voir les erreurs comme des opportunités d’apprentissage. Et c’est ça la clé.

Vous connaissez cette petite voix intérieure qui dit : “Et si je n’étais pas assez intelligent(e) ?” Avec une mentalité de croissance, cette voix devient : “C’est un défi, mais je peux apprendre”. Le changement est subtil, mais puissant.

Passionnante conférence du docteur Carol Dweck. Pour en profiter pleinement si vous n’êtes pas à l’aise en anglais, allez dans les réglages et choisissez sous-titres traduits automatiquement en français.

Pourquoi est-ce essentiel pour apprendre les maths ?

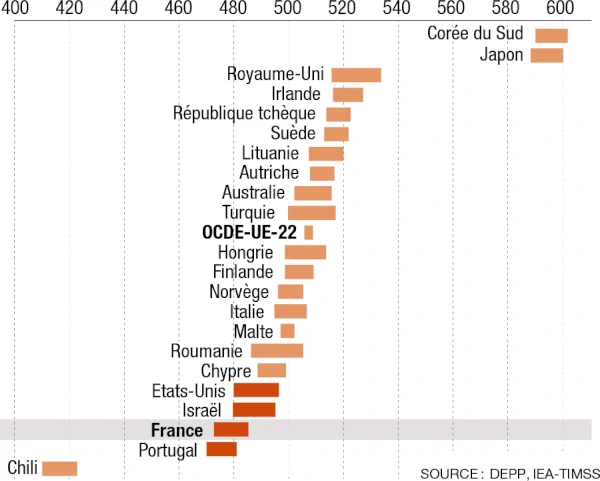
Combien d’élèves se sentent bloqués parce qu’ils pensent ne pas avoir “ce qu’il faut” ? Trop souvent, on associe la réussite en maths à un âge d’or mythique : “Il ou elle est doué(e), moi non”.

Pourtant, personne ne naît génie des maths. Pas même Einstein.

Avec une mentalité de croissance, on comprend que les compétences mathématiques, comme un muscle, se développent avec de l’exercice. Voici quelques raisons pour lesquelles ce mindset change tout :

Les erreurs deviennent des alliées

Une étude célèbre menée par Carol Dweck et ses collègues a révélé que les cerveaux des personnes avec une mentalité d’évolution réagissent de manière différente face aux erreurs. En utilisant des techniques d’imagerie cérébrale, les chercheurs ont observé une activité accrue dans les zones liées à l’apprentissage chez ces individus, même lorsque leurs réponses étaient incorrectes.

Pour eux, une erreur n’est pas un échec irrévocable mais une opportunité d’analyser, de corriger et de comprendre. En réalité, c’est par ce processus d’ajustement que le cerveau construit de nouvelles connexions neuronales. En clair, chaque erreur devient un pas de plus vers la maîtrise

Et pourquoi cela change tout ? Parce que cela transforme la perception de l’échec : au lieu d’être paralysés par la peur de se tromper, les apprenants se sentent encouragés à explorer, tester et repousser leurs limites. Ce simple changement de perspective peut littéralement révolutionner la façon dont nous abordons l’apprentissage – en maths, et bien au-delà !

La persévérance remplace l’impuissance

En maths, il est tentant d’abandonner devant un problème complexe. Prenons l’exemple d’un élève qui bloque sur une équation quadratique. Plutôt que de déclarer « Je ne suis pas fait pour ça », il pourrait essayer une approche différente : dessiner une parabole pour visualiser la solution ou revoir les bases de factorisation. Chaque tentative est une occasion de renforcer ses compétences.

Un autre exemple : imaginez un enfant apprenant ses tables de multiplication. Au lieu de dire « Je suis mauvais en calcul mental », il peut transformer l’apprentissage en jeu avec des cartes flash ou des applications interactives. Peu à peu, ce qui semblait insurmontable devient plus accessible.

La science appuie ce constat. Des études montrent que persévérer, même dans l’erreur, stimule la plasticité neuronale, c’est-à-dire la capacité du cerveau à se reconfigurer pour mieux apprendre. Avec une mentalité d’évolution, l’échec est simplement une étape vers le succès, un signal que le cerveau peut adapter ses stratégies pour aller plus loin. Et c’est là que tout change.

Avec seulement un léger changement d’état d’esprit, un enfant battu d’avance devient un. super-héros des maths.

On développe des stratégies adaptées

Avec un Growth Mindset, on cherche activement des solutions différentes, des moyens alternatifs d’aborder un problème. Et devinez quoi ? C’est exactement ce que demande la résolution de problèmes mathématiques.

Comment l’adopter concrètement dans l’apprentissage ?

OK, très bien, mais comment faire pour cultiver cette fameuse mentalité de croissance, surtout en maths ? Voici quelques pistes pratiques – que vous soyez élève, parent ou enseignant.

Changer son langage

  • Remplacez définitivement (C’est une vraie décision consciente) “Je ne suis pas bon en maths” par “Je ne comprends pas encore”.
  • Ajoutez toujours un “encore” à la fin de vos phrases quand vous parlez de compétences non acquises. Cela change votre perception et celle des autres.

Valoriser les efforts, pas juste les résultats

  • Parents : félicitez l’effort, même si la réponse est incorrecte (“Je vois que tu as cherché une solution originale”).
  • Enseignants : mettez en avant le processus de réflexion des élèves, pas seulement la bonne réponse.

Réinterpréter les échecs

  • Chaque erreur est une donnée. Les plus grands scientifiques, artistes ou inventeurs ne se sont jamais arrêtés à leurs premiers échecs.
  • Faites de vos échecs une opportunité : posez-vous ces deux questions « Qu’est-ce qui n’a pas marché ? » et « Que puis-je changer pour progresser ? ».

Utiliser des ressources adaptées

  • Vidéos explicatives, jeux mathématiques interactifs, groupes de soutien… Les outils ne manquent pas. Si une méthode ne marche pas, essayez-en une autre !

Incorporer l’humour

  • Dédramatisons ! Un problème trop complexe ? Prenez une pause et dites-vous : « Alors là, mon cerveau est au niveau escargot, mais bon, il avance quand même ! ».

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Des maths, des humains et une quête sans fin

Le concept de Growth Mindset nous rappelle que personne n’a un plafond prédéfini hormis celui de nos propres croyances limitantes. Oui, même en maths ! Le plus important, c’est de développer une attitude ouverte face à l’apprentissage, aux erreurs et à soi-même.

Alors, si aujourd’hui vous hésitez encore à croire en vos capacités ou celles de vos enfants, pensez-y : avec un peu de persévérance et une pointe de mentalité de croissance, tout devient possible. Même transformer une aversion pour les maths en… un véritable plaisir ?

Prêts à changer de mindset et à conquérir les maths ? Allez-y, le prochain défi n’attend que vous !

Bibliographie

Le livre de Carol S. Dweck a été traduit en français sous le titre « Changer d’état d’esprit : Une nouvelle psychologie de la réussite » aux éditions Mardaga en mai 2010. Ce livre est disponible en version brochée et en livre audio.
Une édition plus récente, intitulée « Osez réussir ! : Changez d’état d’esprit« , a été publiée en 2021, toujours chez Mardaga.
Ces ouvrages explorent en profondeur le concept de « Growth Mindset » et offrent des conseils pratiques pour adopter une mentalité de croissance dans divers aspects de la vie, y compris l’apprentissage des mathématiques.

Publié le

Maths : 10 astuces pour vaincre la procrastination

Temps de lecture 5 minutes

La procrastination… ce drôle de phénomène qui transforme une petite séance de maths en une montagne infranchissable. Si vous (ou votre ado) remettez toujours vos équations au lendemain, sachez que vous n’êtes pas seuls. C’est humain, presque un sport national chez certains. Le principe est simple : si vous avez un devoir à rendre dans huit jours, c’est toujours plus intéressant d’attendre la veille au soir, histoire de bien paniquer.

Mais si on veut progresser, il faut bien finir par s’y mettre. Alors, laissez-moi vous partager quelques astuces qui ont fait leurs preuves. Vous verrez, ça change tout (ou presque) !

1. Fixez un micro-objectif

Pas de « je vais tout réviser aujourd’hui« . Non. Dites-vous plutôt : « Je vais juste comprendre cette question aujourd’hui. » Ça peut être une petite équation, un graphe… un truc accessible. Et une fois que c’est fait ? On respire, et on peut même enchaîner si on se sent motivé.

Ca me rappelle quand je devais motiver ma fille à faire ses devoirs et qu’elle s’affalait, catastrophée, en se lamentant : « J’y arriverai jamais. J’ai une mon-ta-gne de travail« . Je lui disais : Imagine que tu sois réellement au pied d’une montagne et que tu dois la gravir. Si tu fixes ton regard sur le sommet, si haut, si lointain, tu n’auras qu’une envie : te coucher au bord du chemin et soupirer. Alors essayons une autre attitude.

Baisse les yeux. Tu vois le chemin ? C’est celui qui mène au sommet. Regarde ses petits cailloux, ses pierres proéminentes. Avance ton pied droit puis le gauche, c’est bien. Evite les trous et les bosses, respire et garde le rythme. Tu as vu ? Tu as déjà atteint le premier virage du sentier, sans t’en apercevoir. Allez, continue, le nez au sol. Dans pas longtemps, tu découvriras que tu es arrivée en haut et tu pourras adminrer le paysage.

2. Instaurez une routine agréable

Je sais, « routine », ça sonne ennuyeux. Mais c’est tout l’inverse : imaginez 15 minutes après le dîner, avec un thé ou un chocolat chaud, juste vous et les maths. On associe ça à un moment agréable, et hop, le cerveau s’y habitue. (Et non, Netflix n’est pas une récompense au milieu, désolée.)

3. Pomodoro : l’arme secrète des procrastinateurs

C’est simple et redoutable. 25 minutes de travail, 5 minutes de pause. C’est court, mais efficace. Vous allez voir, c’est comme si les maths devenaient une mission ultra-focus. Bonus : une fois que vous commencez, il est souvent plus facile de continuer.

4. Dites adieu aux distractions

Soyons honnêtes : réviser avec TikTok ou Instagram qui clignotent en arrière-plan, c’est comme essayer de lire en plein concert. Éteignez tout. Oui, même ce groupe WhatsApp qui « ne prend que deux secondes« . Faites-vous une bulle, juste pour les maths.

Même vous, vous le savez : le téléphone est l’ennemi de vos révisions. Alors, de votre propre initiative (parce que c’est insupportable qu’un adulte l’impose), vous l’éteignez (oui, off, pas de mode silencieux, pas de vibreur) et vous le rangez dans le tiroir. Non, pas sur la table. Hors de vue. Ce sera encore plus intéressant de découvrir ce que vous n’avez pas vraiment raté quand vous le rallumerez.

5. Riez de vos erreurs (oui, sérieusement)

Vous avez calculé que 2 + 2 = 22 ? Parfait ! On va pas se mentir : c’est faux. Mais ça veut dire que vous avez essayé. Les erreurs, c’est un tremplin. Relisez, comprenez ce qui a coincé, et passez à la suite. C’est là que l’apprentissage se fait. Et franchement, tout le monde s’est déjà planté. Moi, j’ai un tableau plein d’anecdotes absurdes si vous voulez.

6. Récompensez vos efforts (un petit plaisir, ça motive)

Un problème résolu, une récompense. Ça peut être un biscuit (gaffe au sucre quand même), un épisode de votre série préférée, ou même un simple « bien joué ! » dans votre tête. Parce que oui, vous méritez de célébrer chaque victoire. Mais bon, on évite les croissants au Nutella à chaque addition.

7. Travaillez à plusieurs, mais choisissez bien vos coéquipiers

Rien de pire qu’un partenaire qui parle tout le temps ou regarde son téléphone en douce. Trouvez quelqu’un qui est à votre niveau, ou mieux, un poil au-dessus. Ça aide à progresser, et en bonus, vous riez ensemble quand vous êtes bloqués sur une question tordue.

8. Changez de sujet pour éviter l’ennui

Les maths, c’est vaste. Si les fractions vous donnent des boutons aujourd’hui, passez aux graphes ou aux statistiques. Varier les sujets peut relancer votre intérêt, et en plus, vous progressez sur plusieurs fronts à la fois. Un peu comme un entraînement multi-sports, mais en moins fatigant.

9. Trouvez votre créneau parfait

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Moi, je suis du matin (une fois levée. Mais ça, c’est une autre histoire qui n’intéresse personne ici). D’autres adorent le soir. Trouvez ce moment où votre cerveau est le plus alerte. Et oui, éviter les sessions tardives quand vous êtes déjà en mode zombie, ça compte aussi.

10. Pensez à la vraie raison derrière tout ça

Pourquoi apprenez-vous les maths ? Pas juste pour passer un contrôle, un examen ou embellir votre dossier scolaire pour Parcoursup. Mais pour comprendre comment fonctionne le monde, calculer un pourboire sans stresser, ne pas vous faire avoir dans une négo ou même un jour expliquer à quelqu’un d’autre. Et si ça, ce n’est pas motivant, je ne sais pas ce qui l’est.

Publié le

La répétition espacée pour mémoriser les maths ?

Temps de lecture 7 minutes

Parlons aujourd’hui d’une méthode aussi efficace qu’élégante : la répétition espacée. Vous savez, cette technique qui consiste à réviser intelligemment au lieu de rester collé à son cahier jusqu’à ce que les formules vous dansent devant les yeux comme un écran de veille des années 2000.

Je vais vous montrer comment appliquer cette méthode à l’apprentissage des maths, que vous soyez collégien ou lycéen. Alors, c’est parti pour une plongée dans l’art de ne pas oublier ce qu’on vient d’apprendre !

La répétition espacée : qu’est-ce que c’est ?

Apprendre les mathématiques peut souvent ressembler à une montagne à gravir, avec des notions qui semblent disparaître dès qu’on tourne la page. La répétition espacée est une méthode idéale pour ancrer durablement ces connaissances et progresser de manière efficace. Voici comment elle fonctionne :

La répétition espacée, c’est un peu comme arroser une plante : vous ne videz pas tout votre arrosoir d’un coup (comprenez : réviser tout la veille du contrôle), mais vous donnez juste ce qu’il faut, au bon moment, pour que la plante (votre cerveau) puisse pousser tranquillement.

En clair, il s’agit de réviser les notions à des intervalles de plus en plus longs. Pourquoi ? Parce que c’est ainsi que fonctionne notre mémoire. La première fois que vous apprenez quelque chose, votre cerveau l’oublie rapidement. Mais si vous le revoyez avant que l’oubli soit complet, il le retient mieux. Et ainsi de suite, jusqu’à ce que cela devienne un souvenir durable. Merci Ebbinghaus et sa fameuse courbe de l’oubli !

Supposons que vous ayez un cours aujourd'hui. C'est la pastille rouge. Supposons encore que vous avez écouté et que vous avez l'impression d'avoir tout compris. Vouis êtes sûr de retenir sans effort. Ben non. Regardez la courbe rouge. C'est la courbe de l'oubli. Demain vous ne saurez plius que 50% du cours et presque plus rien dans une dizaine de jours.<br/>Faites une révision intégrale demain (R1) pour remettre votre mémoire au niveau de ce que vous saviez pendant le cours. Puis une autre dans trois jours (R2) et une autre dans 6 jours et peut-être même une dernière dans 12 jours.<br/>Là, oui, vous aurez tout retenu et pour ttrès longtemps. Votre mémoir aura suivi la courbe verte, celle de la mémorisation, du savoir. La répétition espacée pour mémoriser les maths
Supposons que vous ayez un cours aujourd’hui. C’est la pastille rouge. Supposons encore que vous avez écouté et que vous avez l’impression d’avoir tout compris. Vous êtes sûr de retenir sans effort. Ben non. Regardez la courbe rouge. C’est la courbe de l’oubli. Demain vous ne saurez plus que 50% du cours et presque plus rien dans une dizaine de jours.
Faites une révision intégrale demain (R1) pour remettre votre mémoire au niveau de ce que vous saviez pendant le cours. Puis une autre dans trois jours (R2) et une autre dans 6 jours et peut-être même une dernière dans 12 jours.
Là, oui, vous aurez tout retenu et pour très longtemps. Votre mémoire aura suivi la courbe verte, celle de la mémorisation, du savoir.

En termes simples, c’est une technique qui vous aide à « muscler » votre mémoire. Et le meilleur, c’est que cette méthode fonctionne pour tout type d’apprentissage, mais elle est particulièrement puissante en maths.

Pourquoi la répétition espacée est-elle si efficace pour les maths ?

Les maths… Cette belle discipline où tout s’emboîte, mais où tout peut aussi s’effondrer si vous oubliez une petite formule au passage. La répétition espacée est particulièrement utile en maths parce que :

  1. C’est cumulatif : Les notions de maths s’accumulent comme des briques. Si vous avez oublié une brique de base (exemple : Pythagore), vous aurez du mal à bâtir un mur solide (exemple : trigonométrie).
  2. Les maths demandent de la pratique régulière : Il ne suffit pas de lire un théorème pour le comprendre. Il faut le manipuler, encore et encore.
  3. Cela aide à lutter contre la surcharge cognitive : Revisiter régulièrement les notions permet d’éviter d’“empiler” trop de nouvelles informations sans consolider les anciennes.
  4. Elle renforce la compréhension active : La répétition espacée, combinée à des exercices variés, aide à passer de la simple mémorisation à une compréhension approfondie. Vous ne vous contentez pas de réciter une formule, vous comprenez pourquoi elle fonctionne.

En somme, cette méthode s’adapte parfaitement à la nature logique et progressive des mathématiques.

Comment pratiquer la répétition espacée en maths ?

1. Identifiez ce qui doit être révisé

La première étape, c’est de savoir quoi réviser. Voici quelques pistes :

  • Les formules : Aire d’un cercle, théorème de Thalès, trigonométrie, etc.
  • Les démonstrations types : Exemple : Montrer que la somme des angles d’un triangle fait 180°.
  • Les méthodes : Résoudre une équation du second degré, calculer une limite, tracer un graphique.

Pour chaque chapitre, faites une liste de ces éléments. Par exemple, dans un chapitre sur les fonctions, notez les notions essentielles : équations, variations, courbes et tangentes.

2. Organisez vos révisions

Adoptez un calendrier simple et progressif, basé sur les principes de la courbe de l’oubli : lorsque vous révisez une notion juste avant de l’oublier complètement, vous en renforcez la mémorisation de manière optimale. Ces intervalles progressifs permettent de ralentir le déclin naturel de la mémoire tout en consolidant les connaissances.

  • Jour 1 : Vous apprenez la notion.
  • Jour 2 : Vous la revoyez rapidement.
  • Jour 4 : Vous la revalidez avec un exercice.
  • Jour 8 : Vous la revoyez encore une fois.
  • Jour 15 : Vous testez votre maîtrise.

C’est flexible : adaptez les intervalles à votre rythme et à la difficulté des notions.

Alimentée à intervales réguliers, la mémoire peut libérer toute la puissance de ses super-pouvoirs.

3. Créez des fiches efficaces

Les fiches sont un outil puissant. Voici comment les organiser :

  • Fiches pour les formules : Par exemple, une fiche pourrait contenir au recto la formule d’un cylindre (V = πr²h) accompagnée d’une explication claire de chaque terme, et au verso, un exemple chiffré : “Calculez le volume d’un cylindre de rayon 3 cm et de hauteur 5 cm”.
  • Fiches pour les démonstrations : Listez les étapes clés d’une démonstration. Par exemple, pour le théorème de Thalès, incluez un schéma annoté sur le recto et les étapes de la preuve au verso.
  • Fiches pour les erreurs courantes : Notez une erreur typique que vous faites, par exemple “Oublier de multiplier par le coefficient directeur”, et ajoutez au verso la réponse corrigée avec une explication de la solution.

4. Utilisez des outils numériques

Les applications comme Anki ou Quizlet sont parfaites pour appliquer la répétition espacée. Vous pouvez créer des cartes interactives :

  • Question : Quelle est la dérivée de sin(x) ?
  • Réponse : cos(x).

Ces outils permettent de suivre votre progression et de vous concentrer sur vos points faibles.

5. Adaptez les exercices aux révisions

Pour chaque révision, variez les types d’exercices :

  • Au début : Des exercices simples pour fixer les bases.
  • Progressivement : Des problèmes plus complexes pour renforcer votre maîtrise.

Exemple concret pour les collégiens et les lycéens

Prenons l’exemple des formules de trigonométrie (sinus, cosinus, tangente). Voici comment structurer vos révisions :

  1. Créez des fiches :
  • Une fiche avec les valeurs exactes pour 0°, 30°, 45°, 60° et 90°.
  • Une fiche avec les identités trigonométriques principales (cos²(x) + sin²(x) = 1).
  1. Apprenez par étapes :
  • Jour 1 : Répétez les valeurs exactes à l’oral ou écrivez-les.
  • Jour 4 : Faites un exercice simple où vous devez utiliser ces valeurs.
  • Jour 8 : Essayez un exercice plus complexe où vous combinez plusieurs notions.
  1. Testez-vous :
  • Créez un quiz rapide sur ces formules.
  • Réalisez des exercices corrigés pour vérifier votre compréhension.

Les erreurs à éviter

Parce que, oui, même la meilleure méthode peut être mal appliquée :

  1. Ne pas respecter les intervalles : Si vous laissez passer trop de temps entre deux révisions, vous oublierez tout. Inversement, répéter trop souvent peut être contre-productif.
  2. Se contenter de lire : La révision passive (“Je lis ma fiche”) est bien moins efficace que la révision active (“Je résous un exercice”).
  3. Vouloir tout faire d’un coup : Priorisez les notions essentielles.

Compléments et approfondissements

Associer la répétition espacée à d’autres techniques

  • Pratique active : Combinez la répétition avec des exercices variés.
  • Mind maps : Créez des cartes mentales pour visualiser les liens entre différentes notions.
  • Gamification : Transformez vos révisions en jeu (score, défis).
Cette carte mentale, par exemple, reprend toutes les notions à savoir sur les fonctions. La répétition espacée pour mémoriser les maths
Cette carte mentale, par exemple, reprend toutes les notions à savoir sur les fonctions.

Un plan sur l’année scolaire

  • Avant les contrôles : Revoir les notions à intervalles réguliers.
  • Pendant les vacances : Consolider les bases et anticiper les prochains chapitres.
  • Préparation aux examens : Reprendre systématiquement les notions clés depuis le début de l’année.

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Un dernier mot

La répétition espacée, c’est un peu comme l’entretien d’une voiture : il faut y aller régulièrement pour éviter les pannes (ou les trous de mémoire en plein contrôle !). Alors, prenez le temps de structurer vos révisions, soyez patients et, surtout, amusez-vous à constater vos progrès. Vous verrez, les maths deviendront moins intimidantes et bien plus accessibles.

Et si vous avez des questions ou des retours d’expérience, partagez-les dans les commentaires. Je suis là pour vous aider à développer vos super-pouvoirs mathématiques !

Quelques ressources gratuites

Pour vous donner un coup de main et pour vous montrer qu’on peut facilement s’organiser pour être plus efficace dans ses révisions, je vous ai préparé trois petits modèles qui pourraient vous être utiles. Vous êtes libres de les télécharger, de vous en inspirer, de les modifier mais surtout… de vous en servir !

Publié le

Monica Neagoy : rendre les mathématiques accessibles à tous

Temps de lecture 6 minutes


C’est drôle comme la simple évocation du mot « mathématiques » fait fuir certains et briller les yeux des autres. Mais pourquoi ce fossé ? Monica Neagoy, experte en pédagogie et mathématicienne passionnée, s’est donné une mission : rendre les mathématiques accessibles à tous. Ce n’est pas un rêve idéaliste, c’est un projet concret. Armée de la célèbre Méthode de Singapour et d’une pédagogie aussi rigoureuse que ludique, elle parcourt le monde pour rendre les mathématiques accessibles, passionnantes et, osons le dire, carrément cool. Si vous avez croisé son nom récemment – peut-être dans l’émission Quotidien – vous avez sûrement senti son énergie communicative. Mais qui est vraiment Monica Neagoy, et en quoi sa vision révolutionne-t-elle l’apprentissage des maths ? Attachez vos ceintures, on plonge dans un univers où les chiffres prennent vie.

Une vie dédiée aux maths et aux élèves : qui est Monica Neagoy ?

Monica Neagoy n’est pas seulement une mathématicienne. C’est une véritable globe-trotteuse de la pédagogie, une experte qui a passé sa vie à décortiquer les rouages de l’apprentissage des maths pour les rendre accessibles à tous. Née d’une double culture franco-américaine, elle a étudié dans des systèmes éducatifs variés, en Asie, en France et aux États-Unis, où elle a décroché un doctorat en didactique des mathématiques.

Mais ce n’est pas tout. Professeure à l’Université de Georgetown, directrice de projets pour la National Science Foundation à Washington, conférencière internationale… Monica a multiplié les casquettes avec une constante : son amour pour l’enseignement. Son objectif ? Aider les élèves à comprendre les maths profondément, au lieu de les survoler comme on résout des énigmes par automatisme.

Et c’est là qu’intervient sa grande spécialité : la Méthode de Singapour. Depuis plus de deux décennies, Monica défend cette approche révolutionnaire, qui invite les élèves à passer du concret au pictural avant d’aborder l’abstraction. Une méthode qui mise sur la logique et la compréhension, plutôt que sur des techniques de mémorisation à court terme. Mais patience : on vous en parle en détail dans la prochaine section.

Avant d’entrer dans le vif du sujet avec la Méthode de Singapour, une question mérite qu’on s’y arrête : qu’est-ce qui rend Monica Neagoy si unique ? Sa pédagogie, bien sûr, mais aussi son énergie débordante et son sens de la créativité.

La Méthode de Singapour : une révolution pédagogique

La Méthode de Singapour n’est pas juste un effet de mode ; c’est une philosophie de l’apprentissage qui bouscule les codes traditionnels. Et Monica Neagoy en est l’ambassadrice hors pair. Mais au fait, c’est quoi exactement ?

La Méthode de Singapour repose sur l’acquisition d’une notion par nos sens physiques avant de les conceptualiser pour les manier plaus facilement. Comme ici, comprendre une proportionnalité.

Imaginez que vous deviez résoudre un problème comme « Combien de litres d’eau restent dans une piscine après qu’on en ait retiré la moitié ? ». Plutôt que de plonger directement dans les chiffres, la Méthode de Singapour propose trois étapes.

  1. Le concret : manipulez des objets réels, comme des gobelets d’eau.
  2. Le pictural : dessinez la situation avec des schémas simples.
  3. L’abstrait : enfin, passez à la résolution mathématique pure.

Ce passage graduel du tangible à l’abstrait aide les élèves à construire une compréhension solide des concepts. Et ce n’est pas qu’une théorie ! Dans les pays où cette méthode est appliquée, les résultats sont spectaculaires : des élèves plus autonomes, une meilleure capacité de résolution de problèmes et, surtout, un amour retrouvé pour les maths.

Monica Neagoy a adapté cette méthode pour les programmes français avec une série d’ouvrages. Dans L’approche de Singapour – Enseigner les mathématiques avec Monica Neagoy, elle offre des outils concrets aux enseignants. Ces livres regorgent d’exemples pratiques, de situations du quotidien et de conseils pour insuffler une dose de créativité dans chaque leçon.

Mais Monica ne se contente pas de manuels ou de conférences. Elle va plus loin, en ajoutant une touche artistique et théâtrale à ses interventions. Oui, oui, vous avez bien lu : des maths qui montent sur scène !

Quand les maths montent sur scène : l’art au service des chiffres

Si vous pensiez que les maths étaient juste une affaire de tableaux noirs et d’équations sans âme, Monica Neagoy est là pour vous prouver le contraire. En plus d’être mathématicienne, elle a une passion pour l’art et le théâtre. Et elle a eu une idée brillante : mêler les deux.

Avec son célèbre spectacle MathMagic Show, elle fait des maths une expérience interactive et immersive. Le public, qu’il soit composé d’enfants, de parents ou d’enseignants, découvre des concepts mathématiques à travers des jeux, des histoires et même des tours de magie. Oui, magie ! Par exemple, Monica utilise des énigmes géométriques pour émerveiller son public tout en enseignant des notions complexes de manière intuitive.

Mais pourquoi une telle approche ? Parce qu’elle sait que l’émotion joue un rôle clé dans l’apprentissage. L’émerveillement, la curiosité et l’interaction aident les élèves à intégrer les notions plus durablement. Et quoi de mieux qu’un peu de magie pour déclencher cet émerveillement ?

Après avoir exploré cette facette artistique, revenons à l’essentiel : la manière dont Monica inspire enseignants et élèves au quotidien, dans leurs salles de classe.

Un modèle pour enseignants et élèves

Monica Neagoy ne se contente pas de transmettre son savoir. Elle forme aussi des enseignants dans le monde entier. Ses conférences et ateliers, souvent accompagnés de vidéos et de ressources pratiques, permettent aux professeurs de changer leur regard sur les maths.

L’un des messages clés de Monica est de traiter les erreurs comme des opportunités. Trop souvent, les élèves redoutent les erreurs et finissent par détester les maths. Monica, elle, les transforme en points de départ pour des discussions enrichissantes. « Pourquoi ce raisonnement ne fonctionne-t-il pas ? Et si on essayait autrement ? » Ce genre de réflexion aide les élèves à développer leur esprit critique et leur résilience.

Les témoignages abondent : des enseignants disent redécouvrir leur métier grâce à Monica, et des élèves retrouvent confiance en eux. Que ce soit à travers ses livres, ses conférences ou ses spectacles, elle insuffle une véritable passion pour les maths.

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Monica Neagoy est bien plus qu’une experte en pédagogie. Elle est une inspiration, une passeuse de savoir qui rappelle que les maths ne sont pas une montagne infranchissable. Grâce à la Méthode de Singapour, son approche théâtrale et sa bienveillance envers les élèves, elle redéfinit l’apprentissage des mathématiques. Alors, si vous pensez encore que les maths sont ennuyeuses, laissez Monica vous prouver le contraire. Vous pourriez bien vous retrouver à aimer résoudre des équations. Oui, oui, c’est possible.

Publié le

Les erreurs fréquentes en maths : comment les éviter ?

Certaines erreurs sont récurrentes en maths. Heureusement on peut les éviter
Temps de lecture 7 minutes

Ah, les mathématiques ! Ce sujet redouté par certains, adoré par d’autres, mais souvent un véritable casse-tête pour beaucoup d’élèves. On peut avoir un bon prof, des cours intéressants, mais parfois, c’est le petit détail qui nous fait trébucher et perdre des points sur une question simple. Pas de panique : dans cet article, on va passer en revue les erreurs les plus fréquentes que font les élèves en maths et surtout, comment les éviter pour avancer sereinement. Et, spoiler alert : les erreurs sont souvent là où on ne les attend pas !

1. Le travail au coup par coup : quand on se contente du minimum

C’est la fameuse erreur des élèves qui attendent le dernier moment pour réviser, qui n’ouvrent leur cahier que la veille du contrôle… ou pire, qui ne font que les devoirs donnés par le prof sans approfondir leurs connaissances. Vous êtes du genre à faire vos exercices et puis basta ? Vous ne savez peut-être pas que cela peut vous jouer de mauvais tours. Travailler de manière ponctuelle sans révision régulière ne mène pas à la réussite en maths.

🔑 Le conseil : La clé, c’est la régularité. Même si vous n’avez pas de devoirs, passez un peu de temps chaque jour à revoir votre cours et à faire des exercices d’application. Si vous n’avez pas d’exercices donnés en classe, créez-vous des petits défis mathématiques. Cela permet de maintenir une bonne dynamique et de ne pas se retrouver perdu au moment du contrôle.

—

2. Faire les exercices avec le cours sous les yeux : l’illusion de la facilité

Le cerveau est paresseux, et il adore prendre des raccourcis. Si vous faites vos exercices avec le cours sous les yeux, il va logiquement se dire : « Pas besoin de mémoriser, je n’ai qu’à consulter les notes. » Mauvaise idée ! Faire un exercice ne consiste pas à trouver un résultat, mais à tester votre compréhension du cours. Si vous ne vous efforcez pas d’appliquer ce que vous avez appris sans filet, vous ne ferez que reproduire ce que vous avez déjà vu… et vous oublierez l’essentiel : comprendre.

🔑 Le conseil : Essayez de faire vos exercices sans ouvrir le cours, au moins au début. Si vous bloquez, alors consultez, mais seulement pour clarifier un point précis. Vous verrez que plus vous ferez cela, plus vous progresserez et plus vous serez à l’aise pour appliquer vos connaissances de manière autonome.

—

3. « Je travaille suffisamment » : croire que l’on en fait assez

C’est la phrase classique qu’on entend souvent : « Mais j’ai travaillé ! J’ai fait mes devoirs ! » Pourtant, travailler uniquement sur les exercices demandés ne suffit pas toujours. Croire qu’on travaille suffisamment, alors que l’on fait le strict minimum, est une erreur courante. Oui, le travail en classe est important, mais il faut aussi compléter par des révisions, des exercices d’application, et comprendre pourquoi on fait certaines erreurs.

🔑 Le conseil : Une heure de cours = une heure de travail chez soi. C’est ce que les pédagogues recommandent. Si vous avez un cours de maths d’une heure, il vous faudra une heure de révisions et d’exercices. Si vous ne comprenez pas une erreur, ne l’ignorez pas ! Comprendre ce qui cloche est souvent la clé pour avancer.

—

4. Mes erreurs sont « juste » des étourderies

Ah, cette excuse classique : « C’est juste une étourderie, je savais pourtant comment faire ! » Mais attention, cette excuse masque souvent un manque de compréhension d’un concept. Si vous maîtrisez un calcul, vous ne ferez pas d’étourderie ! Si vous oubliez une parenthèse ou vous trompez de signe, cela montre que vous n’avez pas encore bien intégré la méthode.

🔑 Le conseil : Ne sautez pas d’étapes dans vos calculs. Prenez votre temps et soyez rigoureux. Cela vous évitera bien des erreurs et vous fera gagner des points précieux lors des contrôles.

—

5. Oublier les conditions : un théorème, c’est pas magique !

« Ce théorème fonctionne tout le temps, non ? » Non, désolé. Beaucoup d’élèves oublient que les théorèmes ou propriétés ne s’appliquent que sous certaines conditions. Les énoncés ne sont pas là pour faire joli ; ils ont un sens précis, et omettre une condition peut faire échouer toute une démonstration.

🔑 Le conseil : Avant de commencer une démonstration, prenez un instant pour vérifier que toutes les conditions du théorème sont réunies. Cela vous évitera de faire des erreurs de raisonnement et de perdre des points.

—

6. Commencer un exercice sans bien lire l’énoncé

Il y a ceux qui se lancent tête baissée dans un exercice sans vraiment lire l’énoncé. Et là, paf ! Un petit détail dans la question est mal compris, et toute la solution part en vrille. Lire l’énoncé attentivement est crucial pour éviter de commettre des erreurs simples mais fatales.

🔑 Le conseil : Prenez toujours un moment pour lire et relire l’énoncé. Posez-vous des questions pour vérifier que vous avez bien compris : « Que me demande-t-on exactement ? », « Quelles propriétés puis-je utiliser ? », « Quelles informations importantes puis-je extraire de ce texte ? »

—

7. Croire que seul le résultat compte

C’est la grosse erreur qu’on retrouve souvent chez les élèves : « Le résultat est juste, donc peu importe comment j’y suis arrivé. » Eh bien, non ! En maths, le raisonnement est tout aussi important que le résultat. En effet, si vous ne montrez pas comment vous êtes arrivé à votre réponse, le professeur ne saura pas si vous avez réellement compris la méthode.

🔑 Le conseil : Prenez toujours le temps de rédiger vos étapes de manière claire et logique. Cela montre que vous comprenez la méthode et vous permet de ne pas perdre des points en cas d’erreur dans le calcul.

—

8. Se réfugier derrière des excuses : « Il faisait trop chaud, je n’arrivais pas à me concentrer… »

Il est toujours plus facile de se cacher derrière des excuses, mais la vérité, c’est que si vous ne réussissez pas un devoir ou un contrôle, c’est souvent à cause d’un manque de travail ou de préparation. Le facteur environnement n’est qu’une petite partie du problème.

🔑 Le conseil : Ne cherchez pas des excuses externes. Ce qui compte, c’est votre engagement. Si vous avez des lacunes, il est toujours temps de les combler avec du travail et, si nécessaire, avec l’aide d’un prof particulier. Prendre conscience de ses faiblesses, c’est déjà un premier pas vers la réussite.

Les erreurs fréquentes en maths : Les adolescents sont aujourd'hui sollicités par une société trépidante dans laquelle l'information est omniprésente, favorisant une forme de dilettantisme. Le principal défi que doivent relever les élèves est celui de la force morale : rester concentré malgré tout !
Les adolescents sont aujourd’hui sollicités par une société trépidante dans laquelle l’information est omniprésente, favorisant une forme de dilettantisme. Le principal défi que doivent relever les élèves est celui de la force morale : rester concentré malgré tout !

—

9. Croire que tout est perdu quand on manque des bases

« J’ai loupé les bases, c’est foutu ! » Ce genre de pensée peut démoraliser un élève, mais c’est une erreur. Vous pouvez toujours rattraper vos lacunes, même si vous avez pris du retard. Tout est une question d’engagement et de méthode.

🔑 Le conseil : Ne perdez pas espoir. Avec un peu de travail et de patience, vous pouvez combler vos lacunes. En plus, avec l’aide d’un professeur particulier, cela devient beaucoup plus facile et rapide !

—

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Conclusion : Il est temps de transformer vos erreurs en atouts !

Les erreurs font partie du processus d’apprentissage, mais les comprendre et les corriger est ce qui fait toute la différence. Alors, la prochaine fois que vous ferez une erreur, ne paniquez pas : posez-vous les bonnes questions et utilisez-la comme une opportunité pour progresser.

Et si vous avez besoin d’aide pour éviter ces erreurs, je suis là pour vous accompagner et vous guider. Vous êtes prêts à relever le défi ? C’est en travaillant régulièrement et de manière réfléchie que vous réussirez à maîtriser les mathématiques !

—

Si cet article vous a aidé, partagez-le avec vos amis ou inscrivez-vous à ma newsletter pour d’autres conseils et astuces sur les mathématiques. Besoin d’une aide plus personnalisée ? Prenez rendez-vous pour une rencontre avec moi et mettez toutes les chances de votre côté pour réussir !

Publié le

Le soroban : la méthode japonaise pour exceller en calcul mental que la France devrait envisager

le soroban ou boulier japonais
Temps de lecture 7 minutes

Vous avez sans doute regardé ces vidéos sur internet : des écoliers japonais, le regard concentré, tapotant sur un abaque imaginaire comme s’ils maîtrisaient un art martial numérique. En quelques secondes, voilà qu’ils résolvent des multiplications à plusieurs chiffres, le tout plus vite qu’une calculatrice. Cet outil, le soroban, n’est pas seulement un gadget exotique, mais un héritage pédagogique puissant au Japon. Pendant ce temps, en France, les élèves semblent bien plus patauds en calcul mental, et cela se reflète dans les classements internationaux comme le TIMSS (Trends in International Mathematics and Science Study), où nos jeunes ne brillent pas vraiment. Alors, pourquoi un tel fossé ? Et si le remède à nos lacunes en maths se trouvait dans un retour à des pratiques ancestrales comme le soroban ?

Le soroban, un abaque millénaire et ultra-moderne

Avant de plonger dans les enjeux éducatifs, parlons un peu de cet objet magique. Le soroban est un abaque japonais, une évolution du suanpan chinois. Cet outil, bien que simple dans son apparence, est un bijou de logique mathématique.
Composé de tiges verticales sur lesquelles coulissent des boules, le soroban représente les nombres en système décimal. Les colonnes correspondent aux unités, dizaines, centaines, et ainsi de suite, tandis que chaque boule a une valeur déterminée selon sa position.

Mais ne vous méprenez pas : ce n’est pas juste un jouet ancien pour s’amuser en classe. Le soroban calcul mental est une machine à muscler le cerveau. Les élèves qui maîtrisent la méthode Abacus développent une visualisation mentale si précise qu’ils finissent par calculer sans même toucher l’outil, en reproduisant son image dans leur esprit. On appelle cela la méthode du « soroban mental », et c’est là que la magie opère.

En France, où l’on insiste plutôt sur les algorithmes écrits et les calculatrices dès le collège, on pourrait trouver cette approche désuète. Pourtant, des études montrent que travailler avec des méthodes concrètes comme le soroban stimule des parties du cerveau liées à la concentration, à la mémoire et à la logique. Alors, pourquoi ne pas s’en inspirer ?

Avant de débattre des avantages du soroban, intéressons-nous à ce que disent les chiffres… malheureusement peu flatteurs pour la France.

TIMSS : quand la France ne brille pas en maths

En 2019, le TIMSS a confirmé ce que beaucoup redoutaient déjà : la France est à la traîne en mathématiques. Les élèves français se classent parmi les derniers des pays européens, notamment en calcul mental. Les raisons ? Une pédagogie trop abstraite, un manque de pratique régulière et, disons-le, un certain désamour des élèves (et parfois des enseignants) pour la discipline.

Pour comprendre, comparons avec le Japon. Là-bas, les élèves sont confrontés aux maths dès leur plus jeune âge avec des exercices concrets et progressifs. Le soroban joue un rôle essentiel, non seulement pour leur enseigner les bases du calcul, mais aussi pour renforcer leur confiance en leurs capacités. Au lieu de s’effrayer devant un problème complexe, ils le décomposent et l’abordent avec sérénité grâce aux outils qu’ils maîtrisent.

En France, à l’inverse, les méthodes actuelles misent beaucoup sur les outils numériques, mais ces derniers ne stimulent pas suffisamment les processus mentaux. Résultat ? Les élèves peinent à développer une véritable intuition mathématique. L’enseignement semble aussi souffrir d’une approche trop linéaire, où l’on suit un programme sans vraiment personnaliser ou varier les outils.

Mais ne soyons pas fatalistes : et si on s’inspirait du soroban pour réinventer l’apprentissage des maths en France ?

Pourquoi le soroban pourrait révolutionner l’enseignement en France ?

Intégrer le soroban dans les écoles françaises pourrait transformer l’approche des maths de plusieurs manières :

1. Une pédagogie ludique et engageante
Le soroban, avec son aspect visuel et manipulatif, capte l’attention des élèves. C’est bien plus engageant que des colonnes de chiffres tracées sur un tableau. En manipulant un objet concret, les enfants comprennent mieux les concepts abstraits comme les retenues ou les divisions. Ils jouent avec les maths, littéralement.

2. Une meilleure concentration et mémoire
La pratique du soroban demande une attention soutenue. Chaque erreur se reflète immédiatement sur l’abaque, obligeant l’élève à se corriger. De plus, lorsqu’ils passent au soroban mental, les enfants visualisent des opérations complexes, ce qui stimule la mémoire à court et long terme. En comparaison, les outils numériques tendent à externaliser ces fonctions.

3. Des compétences transférables
Apprendre avec un soroban ne se limite pas à résoudre des équations. Cette méthode développe des compétences utiles dans tous les domaines : persévérance, gestion des erreurs, et capacité à diviser un problème complexe en étapes simples.

Et cerise sur le gâteau : plusieurs enseignants français qui ont expérimenté le soroban rapportent un effet inattendu mais bienvenu. Les élèves qui, au départ, rechignaient devant les maths finissent par les adorer, car ils prennent plaisir à voir leurs progrès. Et ça, c’est un vrai changement de paradigme !

Cette vidéo (un reportage France3 Grand-Est) montre une compétition de calcul mental organisée par l’Académie des petits génies à Strasbourg. Des enfants de 5 à 15 ans, venus de différents pays, ont participé à cette compétition. Ils utilisent une méthode de calcul mental appelée « abacus« , qui consiste à manipuler mentalement un boulier. Cette méthode permet de calculer très rapidement des additions, soustractions, multiplications et divisions. La vidéo montre des enfants en train de calculer à toute vitesse, en bougeant leurs doigts devant leur visage. Certains enfants sont capables de calculer en moins d’une seconde ! La vidéo souligne également l’importance de l’entraînement et de la concentration pour réussir dans cette discipline.

Si le soroban a tant à offrir, pourquoi ne l’a-t-on pas encore intégré en France ? La réponse se trouve peut-être dans notre rapport culturel aux maths et à l’éducation.

Les obstacles et les solutions pour intégrer le soroban en France

Un problème de tradition éducative
En France, l’éducation repose encore sur un certain élitisme intellectuel. Les maths sont souvent enseignées de manière abstraite et théorique, comme une discipline destinée à sélectionner les meilleurs. Introduire le soroban, vu comme un outil « simple », pourrait être perçu comme un pas en arrière. Pourtant, les performances japonaises montrent qu’un retour au concret est tout sauf simpliste.

Un manque de formation des enseignants
Pour intégrer le soroban, il faudrait former les professeurs à son usage, ce qui demande du temps et des ressources. Mais ce n’est pas une mission impossible : des associations comme La Maison des Sorobans en France proposent déjà des ateliers. Avec une volonté politique et pédagogique, cela pourrait devenir une réalité dans les classes.

Une solution : commencer tôt et progressivement
Pourquoi ne pas introduire le soroban dès l’école primaire, en complément des outils traditionnels ? Les jeunes enfants sont naturellement attirés par les manipulations concrètes. En parallèle, on pourrait développer des programmes de formation pour les enseignants, avec des exemples inspirants venus du Japon.

Enfin, le soroban ne serait pas seulement une solution pour le calcul mental : il pourrait devenir un symbole d’innovation pédagogique, attirant l’attention des élèves et leur donnant confiance en leurs capacités.

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Le soroban, un outil du passé pour les maths de demain ?

Alors que la France cherche des solutions pour améliorer ses performances en mathématiques, pourquoi ne pas s’inspirer de l’exemple japonais ? Le soroban, à la fois simple et révolutionnaire, pourrait non seulement aider nos élèves à exceller en calcul mental, mais aussi changer leur rapport aux maths en général. Avec un peu de volonté, cette méthode pourrait être intégrée dans nos écoles et permettre à la France de retrouver sa place dans les classements internationaux.
Et qui sait ? Peut-être que dans quelques années, ce seront des écoliers français qui émerveilleront le monde avec des vidéos de calcul mental ultra-rapide. En attendant, sortons nos abaques !

Publié le

Les Nombres Premiers : Ces Énigmes Mathématiques qui Sécurisent Votre Monde

Les nombres premiers sont les stars des mathématiques. Comme les acteurs principaux d’un film, ils peuvent sembler simples à première vue, mais leur importance dépasse l’écran. Définis comme des nombres entiers divisibles uniquement par eux-mêmes et par 1, ils sont les fondations de notre système numérique. On les utilise, souvent sans le savoir, dans tout ce qui touche à la cryptographie, les codes secrets et même la théorie musicale.

Mais revenons à leurs bases. Prenez un nombre comme 126 : vous pouvez le décomposer en \(2 \times 3 \times 3 \times 7\) , où chaque facteur est un nombre premier. Cette propriété, appelée factorisation unique, est si fondamentale qu’elle est au cœur de nombreux systèmes mathématiques modernes. Sans ces briques de base, l’édifice des entiers s’effondrerait.

Ce qui fascine les mathématiciens, c’est leur répartition. Si vous regardez la liste des premiers nombres premiers – 2, 3, 5, 7, 11, etc. –, elle semble aléatoire. Entre deux d’entre eux, vous trouverez parfois un grand vide, et parfois des successions presque collées. Pourquoi ? Nul ne le sait vraiment. Cécile Dartyge, chercheuse en arithmétique, explique : « On sait qu’il existe des intervalles arbitrairement grands sans aucun nombre premier, mais leur répartition reste un mystère ». Ce caractère imprévisible en fait une source inépuisable d’interrogations.

Certains les comparent aux étoiles : apparemment dispersées au hasard, leurs positions suivent pourtant des règles fondamentales que nous essayons de comprendre depuis des siècles. Une analogie que la science adore, car, comme pour les étoiles, l’infini est leur seule limite.

Mais si ces mystères vous intriguent, attendez de découvrir jusqu’où la technologie nous emmène pour explorer ces géants numériques.

La Chasse aux Géants : Quand les Maths rencontrent la Technologie

Le plus grand nombre premier connu à ce jour possède… 41 millions de chiffres. Imaginez-le : il faudrait remplir 10 423 pages A4 pour l’écrire entièrement. Ce mastodonte a été découvert grâce au projet collaboratif GIMPS, qui utilise la puissance des ordinateurs pour détecter de nouveaux premiers de Mersenne. Ces nombres prennent une forme particulière, \(2^p – 1\), où \(p\)est aussi un nombre premier. Leur structure simplifie les tests de primalité.

Mais pourquoi chasser ces colosses ? C’est à la fois un défi intellectuel et une aventure collective. Luke Durant, l’un des participants au projet, raconte : « C’est un peu comme chercher une aiguille dans une botte de foin. Mais quand on la trouve, c’est une victoire partagée par toute une communauté ». GIMPS montre comment des amateurs et des chercheurs peuvent collaborer grâce aux outils numériques, rendant les mathématiques accessibles à tous.

Les nombres premiers géants ne sont toutefois qu’un petit échantillon parmi une infinité encore inexplorée. Une quête sans fin ? Peut-être. Mais chaque nouvelle découverte éclaire un peu plus les mystères des nombres premiers. Par ailleurs, ces découvertes ne sont pas qu’académiques : elles influencent directement la sécurité de vos données.

Cryptographie et Nombres Premiers : Votre Bouclier Numérique

Depuis les années 1970, les nombres premiers ont révolutionné le monde de la cryptographie. C’est grâce à eux que vos données bancaires restent confidentielles. Tout repose sur une idée simple : multiplier deux grands nombres premiers est facile, mais retrouver ces nombres à partir du produit est incroyablement difficile.

Prenons un exemple. Si je vous dis que 34 833 059 est le produit de deux nombres premiers, combien de temps vous faudrait-il pour retrouver 4 421 et 7 879 ? Une éternité ! Maintenant, imaginez des nombres de 300 chiffres. Même les ordinateurs les plus puissants mettraient des centaines d’années à résoudre ce casse-tête.

Le chiffrement RSA, qui repose sur ce principe, est devenu un standard pour sécuriser les communications. Plus la puissance des ordinateurs augmente, plus il est nécessaire d’utiliser des nombres premiers gigantesques pour maintenir la sécurité. Ainsi, des géants comme \(2^{136279841} – 1\)— c’est le tout dernier nombre premier qui vient d’être découvert — pourraient un jour protéger vos transactions.

Anne-Gwénaëlle de Roton, mathématicienne, précise : « L’étude des nombres premiers nous permet aussi d’évaluer la robustesse des systèmes de chiffrement. C’est une course contre la montre entre les chercheurs en sécurité et ceux qui tentent de casser ces codes. » Les nombres premiers, loin d’être de simples curiosités mathématiques, sont ainsi vos gardiens invisibles.

Pourtant, leur rôle en cryptographie n’est qu’un chapitre de leur histoire.

Mystères et Révélations : L’Hypothèse de Riemann et Au-Delà

La fonction zêta de Riemann posséde une partie réelle et une partie imaginaire. La répartition des nombres premiers serait liée aux zéros de cette fonction.
La fonction zêta de Riemann posséde une partie réelle et une partie imaginaire. La répartition des nombres premiers serait liée aux zéros de cette fonction.

Au cœur des recherches actuelles se trouve l’hypothèse de Riemann, une conjecture qui, si elle était prouvée, révolutionnerait notre compréhension des nombres premiers. Formulée en 1859, elle reste l’un des « problèmes du millénaire » non résolus, avec une récompense d’un million de dollars pour quiconque la démontrera. Cette hypothèse cherche à expliquer la répartition des nombres premiers, offrant une clé pour percer leur mystère.

Récemment, des avancées ont été réalisées par des chercheurs comme Larry Guth (MIT) et James Maynard (Oxford). Leurs travaux, bien que non encore validés, permettent d’affiner notre compréhension de la répartition des nombres premiers. Ces progrès rappellent que les mathématiques sont une science vivante, où chaque découverte ouvre de nouvelles portes.

Saviez-vous que… ?

  • Les nombres premiers sont partout : Ils interviennent même dans des domaines inattendus comme la musique, où ils définissent des intervalles harmoniques.
  • Un défi mondial : Le plus grand nombre premier de Mersenne a été découvert grâce à un réseau mondial d’ordinateurs personnels. Vous pourriez contribuer en rejoignant GIMPS !
  • Un problème ancien : Euclide a démontré l’infinité des nombres premiers… il y a plus de 2 300 ans.

Une Fenêtre sur l’Infini

Les nombres premiers sont bien plus que des abstractions mathématiques ; ils incarnent l’essence de l’exploration humaine. À travers leur étude, nous plongeons dans des questions fondamentales sur l’ordre et le chaos, le fini et l’infini. Ils protègent vos données, inspirent les chercheurs et nous rappellent que, même dans un monde de certitudes numériques, il reste de vastes territoires à découvrir.

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Liens suggérés

Publié le

Concentration maximale : Organisez votre espace pour réussir

un environnement de travail idéal pour étudier.

La concentration… Ce Graal insaisissable ! Entre les notifications incessantes, les voisins trop enthousiastes avec leur perceuse, et ce besoin irrépressible de vérifier si les chatons d’Internet vont bien, rester focalisé est devenu un vrai défi. Pourtant, créer un environnement propice à la concentration maximale est moins compliqué qu’il n’y paraît. Avec quelques ajustements astucieux et un soupçon de discipline, vous pouvez transformer votre espace en une bulle dans laquelle votre cerveau carbure à plein régime.

Que vous soyez étudiant noyé sous les formules de mathématiques ou un parent en quête d’optimisation de l’espace d’étude de votre enfant, cet article est pour vous. On vous donne les clés pour aménager un environnement idéal, réduire les distractions, et vous concentrer comme jamais.

Et surtout, débarrassez-vous de cette idée saugrenue qui voudrait que le désordre soit la marque des rebelles et des esprits brillants. En fait, le désordre n’est rien de plus que… du désordre et un obstacle inutile.

L’ordre extérieur contribue à la paix intérieure.

Gretchen Rubin, auteure de The Happiness Project.

Le sanctuaire d’une concentration maximale commence par un bon tri

La base d’un espace propice à la concentration ? L’ordre. Si votre bureau ressemble davantage à un champ de bataille qu’à un espace de travail, il est temps de retrousser vos manches.

Pourquoi le désordre perturbe-t-il autant ?

Votre cerveau est comme un ordinateur : trop de fenêtres ouvertes, et il ralentit. Les objets inutiles sur votre bureau captent involontairement votre attention. Une tasse vide ici, un bloc-notes abandonné là, et vous voilà distrait. Pire encore : le désordre visuel alimente une sensation d’encombrement mental.

Le tri express en 3 questions

  1. En ai-je vraiment besoin maintenant ?
  2. Est-ce que cet objet m’inspire ou me distrait ?
  3. A-t-il une place précise ?

Jetez sans pitié ce qui ne répond pas à ces critères, puis rangez ce qui reste. Un bureau épuré ne signifie pas austérité : une petite plante ou une photo inspirante, et votre espace devient chaleureux sans être envahissant.

Une fois le tri effectué, encore faut-il que cet espace ordonné reste zen. Et cela passe par une gestion intelligente du bruit et de l’ambiance.

Silence, on travaille ! L’importance de l’acoustique

Un voisin bruyant ou un chien qui aboie peuvent transformer votre séance de travail en cauchemar. Pourtant, maîtriser l’environnement sonore est plus accessible qu’il n’y paraît.

Pourquoi le bruit est-il l’ennemi du focus ?

Le cerveau est naturellement curieux. Au moindre son, il tend l’oreille, quitte à interrompre vos pensées. C’est un héritage de nos ancêtres préhistoriques, toujours prêts à détecter un danger. Aujourd’hui, ce mécanisme nous joue des tours face à un klaxon ou un collègue qui mâche un peu trop bruyamment.

Des solutions concrètes pour dompter le bruit

  • Les écouteurs ou casques antibruit : Parfait pour créer une bulle sonore. Et si vous n’aimez pas le silence absolu, essayez les playlists de bruit blanc ou de musique instrumentale.
  • Les panneaux acoustiques : Un petit investissement pour un grand résultat. Ces panneaux absorbent les bruits parasites et embellissent souvent votre décor.
  • Un signal pour votre entourage : Une porte fermée ou un petit panneau « Ne pas déranger » peut suffire à sensibiliser les autres à votre besoin de calme.

Bonus : Le pouvoir du bruit blanc
Les bruits blancs, comme le son des vagues ou un ventilateur, masquent les sons parasites et favorisent un état d’apaisement. Testez des applications comme Noisli ou Rainy Mood pour découvrir ce qui vous aide le mieux à vous concentrer.


Une fois les bruits maîtrisés, il est temps de s’attaquer à un autre sens généralement négligé : la lumière.

Lumière sur l’éclairage favorable à une concentration maximale

Avez-vous déjà tenté de travailler dans une pièce sombre ? C’est comme essayer de lire dans une grotte. La lumière joue un rôle clé dans notre capacité à nous concentrer.

Un bureau en désordre, source de distraction.
Un bureau parfait pour étudier dans de bonnes conditions de concentration maximale.

Environnement de travail, lequel est le vôtre ?

Naturelle ou artificielle : Quelle lumière privilégier ?

  • Lumière naturelle : Idéale pour la concentration, elle stimule la production de sérotonine, l’hormone de la bonne humeur. Placez votre bureau près d’une fenêtre, mais évitez l’éblouissement direct.
  • Lumière artificielle : Optez pour une lampe de bureau avec une lumière blanche et froide (entre 4000 et 5000 Kelvin). Cette température de couleur simule la lumière du jour et maintient votre vigilance.

Les erreurs à éviter

  • Un éclairage trop faible qui fatigue vos yeux.
  • Une lumière jaune et tamisée, plus propice à la détente qu’à la productivité.
  • Des ombres gênantes causées par une source mal positionnée.

Un peu de tech pour améliorer l’ambiance

  • Les ampoules connectées vous permettent d’ajuster la lumière selon vos besoins.
  • Les écrans dotés de filtres anti-lumière bleue réduisent la fatigue oculaire si vous travaillez longtemps.

Maintenant que votre espace est lumineux, passons à un aspect souvent sous-estimé : la gestion des distractions numériques.

Section 4 : L’ennemi invisible : maîtriser les distractions numériques

On y est : le téléphone. Cet outil génial est aussi le roi des distractions. Pas de panique, quelques astuces suffisent pour reprendre le contrôle et éviter la procrastination.

Le piège des notifications

Chaque vibration ou ding détourne votre attention. Même si vous ne répondez pas, il vous faut parfois plusieurs minutes pour replonger dans votre tâche.

Des astuces pour ne plus tomber dans le panneau

  • Activez le mode « Ne pas déranger » : Votre téléphone sera silencieux, sauf pour les appels urgents.
  • Utilisez des applications de blocage : Forest ou Focus@Will limitent l’accès aux réseaux sociaux et vous encouragent à rester concentré.
  • Éloignez votre téléphone : Le placer hors de portée peut suffire à réduire son attrait.

Et pour les distractions en ligne ?

Installez des extensions comme StayFocusd ou LeechBlock pour limiter les sites chronophages. Pensez également à désactiver les notifications sur votre ordinateur.

Une fois votre espace numérique sous contrôle, il ne vous reste plus qu’à adopter ces habitudes au quotidien pour ancrer un véritable rituel de concentration.

Un environnement, un esprit pour une concentration maximale

Créer un espace idéal pour se concentrer n’est pas qu’une question de rangement ou d’éclairage, mais un véritable investissement dans votre bien-être mental. En combinant ordre, silence, lumière et discipline numérique, vous pouvez faire de chaque séance de travail une expérience productive et apaisante.

Alors, prêt à transformer votre coin bureau en sanctuaire de la concentration ? Une fois que tout est en place, vous verrez que même les mathématiques les plus complexes deviennent un jeu d’enfant. Maintenant, à vous de jouer : commencez par une petite action aujourd’hui, et voyez la magie opérer.

Pour aller plus loin : « 4 astuces pour un espace de travail sain promouvant la concentration« 

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Publié le

La France à la traîne en maths : causes, solutions et lueur d’espoir

Il est temps que la France se mette au travail pour redresser collectivement son niveau en mathématiques.

Imaginez un classement où chaque élève de plusieurs pays passe le même examen, un test universel en mathématiques et en sciences. Le TIMSS (Trends in International Mathematics and Science Study) est exactement cela : une photographie quadriennale des performances scolaires à travers le monde. Et cette année, la France brille… par son absence dans le haut du tableau. Dernière en mathématiques parmi les pays européens, elle décroche le bonnet d’âne.

Alors, catastrophe nationale ? Faut-il blâmer les méthodes pédagogiques, les élèves, ou les enseignants ? Pas si vite. Avant de ressortir les grands discours ou d’accabler qui que ce soit, plongeons dans ce que mesure vraiment TIMSS, ce qu’il dit (et ne dit pas), et comment nous en sommes arrivés là. Et surtout, voyons ce que chacun peut faire, individuellement, pour progresser. Parce que oui, il y a des solutions !

TIMSS : Une boussole mondiale pour évaluer les apprentissages

Le TIMSS est un classement international administré tous les quatre ans, conçu pour mesurer les performances des élèves de CM1 et de 4ᵉ en mathématiques et en sciences. Créé dans les années 1990, ce test examine les compétences fondamentales : le calcul, la résolution de problèmes, le raisonnement logique, et les connaissances scientifiques de base.

Comment ça marche ?

Le TIMSS ne se limite pas à évaluer les notes des élèves. Il analyse aussi les contextes éducatifs :

  • La qualité des programmes scolaires.
  • Les méthodes pédagogiques employées par les enseignants.
  • Le climat scolaire et l’engagement des élèves.

En d’autres termes, il ne mesure pas seulement ce que les élèves savent, mais aussi comment et dans quelles conditions ils apprennent. Autant dire que c’est un outil précieux pour comparer les systèmes éducatifs mondiaux.

Et les résultats dans le temps ?

La France, hélas, a souvent fait pâle figure au TIMSS. Depuis les années 2000, ses résultats stagnent ou régressent, tandis que d’autres pays européens progressent. À titre de comparaison, les pays asiatiques comme Singapour, la Corée du Sud et le Japon dominent systématiquement les classements. En Europe, des pays comme la Finlande ou les Pays-Bas tiennent le haut du pavé grâce à des approches pédagogiques innovantes et des investissements conséquents dans l’éducation.

Les résultats du TIMMS de 2023 sont édifiants. La France est avant-dernière du classement.

Mais cette année, le constat est encore plus dur pour la France : elle finit dernière en Europe. Comment expliquer cette contre-performance ?

La France à la traîne : un échec collectif ou mal compris ?

Les résultats du TIMSS 2023 placent la France en bas de l’échelle européenne en mathématiques. Une première question vient à l’esprit : qu’est-ce qui cloche ?

Des chiffres qui dérangent

En 2023, les élèves français de CM1 affichent des scores largement inférieurs à la moyenne européenne, notamment sur des compétences de base comme les fractions, la géométrie simple, et les résolutions de problèmes. Les élèves de 4ᵉ ne font guère mieux : un déficit majeur en raisonnement logique et en algèbre les pénalise.

Mais attention à ne pas tirer sur le messager. Ces résultats sont certes peu glorieux, mais ils ne sont pas le reflet d’une incapacité des élèves français. Ils pointent surtout des failles structurelles. Ce n’est pas une question de talent ou de potentiel, mais d’encadrement et de méthode.

Les causes : une histoire de (mauvaises) solutions

Depuis des décennies, les gouvernements successifs tentent d’enrayer cette spirale descendante, mais force est de constater que les résultats ne suivent pas. Pourquoi ?

1. Des programmes scolaires trop lourds et théoriques

Le programme français est réputé pour être dense et ambitieux. Le problème ? Il s’attarde souvent sur des notions complexes sans accorder assez de temps à l’assimilation des bases. Résultat : les élèves manquent de maîtrise sur les fondamentaux et se retrouvent perdus devant des concepts plus avancés.

2. Un manque de formation des enseignants

Les professeurs de mathématiques sont souvent brillants, mais leur formation pédagogique laisse parfois à désirer. Transmettre un savoir n’est pas inné, surtout lorsqu’il s’agit d’expliquer des concepts abstraits à des élèves ayant des niveaux très disparates.

3. L’effet « anti-maths » dans la société française

Soyons honnêtes : les maths n’ont pas bonne presse en France. Combien de fois entend-on « Moi, les maths, ce n’est pas mon truc » ou « Je n’ai jamais été doué pour ça » ? Ce désamour se transmet parfois des parents aux enfants, créant un cercle vicieux où les élèves ne se sentent pas capables de réussir.

4. Des réformes mal ciblées

Les différentes réformes du système éducatif, qu’il s’agisse de la réduction des heures de maths ou de la refonte des programmes, ont souvent eu l’effet inverse de celui escompté. En cherchant à alléger, on a fini par déséquilibrer.

Changer la donne : une révolution individuelle

Certes, les gouvernements ont leur part de responsabilité, mais tout n’est pas perdu. Les maths, contrairement à une idée reçue, ne sont pas une science réservée aux « génies ». Avec la bonne méthode et un peu de persévérance, tout le monde peut progresser.

1. Prendre les choses en main

Le premier pas pour améliorer ses résultats, c’est de changer son attitude face aux maths. Plutôt que de les voir comme une montagne infranchissable, il faut les aborder comme un puzzle à résoudre. Cela demande du travail, mais aussi une curiosité active.

2. Investir dans les bonnes méthodes

Un professeur particulier peut faire des miracles. Contrairement aux cours en classe, un enseignement personnalisé permet de cibler précisément les lacunes d’un élève. Avec des exercices adaptés et un suivi régulier, les progrès deviennent rapidement visibles.

3. Ne pas viser juste des notes, mais une vraie compréhension

Apprendre les maths ne consiste pas simplement à réciter des formules. Il s’agit de comprendre les concepts derrière les chiffres. En adoptant une méthode qui privilégie le raisonnement et la réflexion, les élèves peuvent non seulement améliorer leurs résultats, mais aussi développer des compétences utiles dans d’autres domaines.

Rien n’est joué, tout est possible

Les résultats du TIMSS 2023 sont un coup de semonce pour la France, mais pas une fatalité. Ce classement met en lumière des faiblesses structurelles et culturelles qui doivent être corrigées, mais il rappelle aussi que chacun peut jouer un rôle dans ce changement. Avec des efforts individuels, des méthodes adaptées, et un peu d’amour pour les maths, les choses peuvent évoluer.

Alors, à tous ceux qui redoutent les équations et les pourcentages : ne baissez pas les bras. Avec de la motivation et le bon accompagnement, même un bonnet d’âne peut finir en tête de classe.

Pourquoi est-il crucial qu’une nation excelle en mathématiques ?

Les mathématiques ne sont pas qu’un exercice intellectuel pour résoudre des équations ou dessiner des graphiques. Elles forment la pierre angulaire du progrès scientifique, technologique, et industriel. Sans un solide socle mathématique, une nation ne peut espérer être un acteur clé sur la scène mondiale. Et les preuves s’accumulent : là où les maths reculent, l’innovation et la compétitivité industrielle s’effondrent.

Des maths, sinon rien : les sciences à l’arrêt

Les mathématiques sont la langue des sciences. Physique, chimie, biologie, informatique… toutes ces disciplines reposent sur des outils mathématiques. Que serait la conquête de l’espace sans les calculs précis des trajectoires orbitales ? Que deviendraient les technologies médicales sans les modélisations mathématiques des virus ou des traitements ? Une nation en déficit mathématique freine automatiquement sa capacité à innover et à contribuer aux grandes découvertes.

Technologie et industrie : les maths, moteur de la compétitivité

L’industrie du XXIᵉ siècle est une industrie technologique. Que ce soit dans la conception d’intelligences artificielles, la programmation d’algorithmes ou encore l’ingénierie avancée, les compétences mathématiques sont incontournables. Or, l’Europe, autrefois au sommet de l’échiquier industriel mondial, perd aujourd’hui son leadership. Pourquoi ? Parce que des nations comme la Chine, la Corée du Sud, ou encore Singapour, ont compris depuis longtemps que la clé de l’avenir réside dans l’éducation aux mathématiques. Ces pays forment des générations entières d’ingénieurs et de scientifiques prêts à relever les défis technologiques de demain. Pendant ce temps, l’Europe peine à fournir suffisamment de profils qualifiés.

Les maths : un levier pour l’emploi et la souveraineté

Au-delà du prestige scientifique, les mathématiques jouent aussi un rôle économique stratégique. Une nation compétente en maths attire des entreprises de pointe, crée des emplois dans des secteurs d’avenir et assure sa souveraineté technologique. En revanche, une nation qui abandonne les maths devient dépendante des innovations étrangères et des brevets déposés ailleurs. Elle perd sa capacité à produire localement et à décider de son propre futur économique.

L’exemple asiatique : l’école des leaders

Depuis plusieurs décennies, l’Asie a fait des mathématiques une priorité nationale. Dans ces pays, les élèves sont formés dès le plus jeune âge à raisonner de manière logique et rigoureuse. Ce travail de fond porte ses fruits : aujourd’hui, ce sont eux qui mènent la danse en matière d’intelligence artificielle, de technologies vertes, ou encore de médecine de pointe. Pendant ce temps, l’Europe reste spectatrice, freinée par un déficit de compétences mathématiques criant.

👉 Les maths ne sont donc pas qu’un « savoir scolaire ». Elles sont un enjeu stratégique, un levier pour l’innovation, la compétitivité économique, et la souveraineté technologique. Si la France et l’Europe veulent reprendre leur place sur l’échiquier mondial, elles devront redonner aux maths la place qu’elles méritent dans l’éducation. Parce qu’en fin de compte, il n’y a pas de progrès sans chiffres.

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

Dernière minute !
Le CNRS se penche sur la faiblesse des Français en maths

L’organisme public de recherche lance ce lundi une consultation citoyenne sur la place des mathématiques dans la société. Les élèves français sont parmi les moins bons de l’Union européenne, selon une étude récente.

Publié le

Les intelligences multiples et les maths : quel type d’apprenant êtes-vous ?

Il existe 8 façon différentes d'aborder la connaissance et de se l'approprier.

L’apprentissage des maths est souvent perçu comme un chemin semé d’embûches, de formules mystérieuses et de calculatrices énigmatiques. Mais que diriez-vous si votre manière d’apprendre dépendait moins de votre « niveau » que de votre type d’intelligence ? Oui, vous avez bien lu : la théorie des intelligences multiples d’Howard Gardner peut transformer votre approche des maths et vous aider à progresser. Explorons comment exploiter vos talents naturels pour devenir un maître des équations… ou simplement vaincre cette fichue peur des fractions.

1. Intelligence linguistique : traduisez les maths en mots

L’intelligence linguistique se manifeste par une aisance avec les mots, tant à l’oral qu’à l’écrit. Les individus dotés de cette intelligence excellent dans la lecture, l’écriture, la narration et l’apprentissage des langues. Ils sont généralement sensibles aux nuances de signification, à la structure des phrases et au rythme des mots.

Vous aimez les jeux de mots, les histoires captivantes et les nuances du langage ? Si les mots sont votre fort, transformez les maths en récits et en conversations.

Comment ça marche ?

  • Mettez les concepts en mots : au lieu de mémoriser mécaniquement des formules, écrivez-les comme une histoire. Par exemple, la formule du périmètre d’un cercle P=2πr devient : « Imagine que tu parcours le bord d’un cercle. Tu fais deux fois le rayon et tu multiplies ça par le nombre magique π ! »
  • Débattez des maths : expliquez un problème mathématique à quelqu’un d’autre. Rien de tel que de parler pour mieux comprendre.
  • Utilisez des métaphores : décrivez les fractions comme des parts de pizza ou les équations comme des balances à équilibrer.

Exemple pratique :

Prenez le théorème de Pythagore. Plutôt que de réciter bêtement : « Dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés », racontez : « Pythagore, ce génie grec, a découvert que si tu fais un carré parfait sur chaque côté d’un triangle rectangle, le grand carré correspond toujours à l’addition des deux petits. »

Les mots vous éclairent ? Voyons si les chiffres et la logique vous captivent encore plus…

2. Intelligence logico-mathématique : plongez dans les défis logiques

Cette forme d’intelligence concerne la capacité à analyser des problèmes de manière logique, à effectuer des opérations mathématiques et à enquêter scientifiquement. Les personnes avec une forte intelligence logico-mathématique sont habiles à reconnaître des modèles, à raisonner déductivement et à penser de manière conceptuelle.

Ah, la logique et les maths, un duo inséparable ! Si vous aimez résoudre des casse-têtes, repérer des motifs et comprendre comment les choses fonctionnent, les maths sont votre royaume.

Si votre esprit fonctionne ainsi, tous les jeux d'esprit vous aideront à mémoriser et à progresser.
Si votre esprit fonctionne ainsi, tous les jeux d’esprit vous aideront à mémoriser et à progresser.

Comment ça marche ?

  • Cherchez des schémas : observez les régularités dans les séries de nombres, les graphiques ou les suites mathématiques.
  • Rendez les maths interactives : essayez des jeux comme Sudoku, des casse-têtes logiques ou des applications d’apprentissage mathématique.
  • Décomposez les problèmes complexes : analysez les étapes d’un problème comme vous le feriez pour une enquête policière.

Exemple pratique :

Pour comprendre les pourcentages, imaginez que vous faites du shopping pendant les soldes. Une réduction de 30 % ? C’est presque un tiers en moins. Vous visualisez votre problème comme une transaction et le tour est joué.

Si les schémas et les chiffres vous fascinent, attendez de voir ce que votre imagination peut accomplir avec l’intelligence spatiale !

3. Intelligence spatiale : visualisez les maths

L’intelligence spatiale implique la capacité à penser en trois dimensions. Cela inclut la sensibilité aux couleurs, aux lignes, aux formes, aux espaces et aux relations entre ces éléments. Les individus avec une forte intelligence spatiale ont une bonne perception des objets dans l’espace et peuvent manipuler ces images mentalement.

Vous aimez dessiner, rêver en trois dimensions ou visualiser des formes ? L’intelligence spatiale est une alliée puissante pour conquérir les maths.

Comment ça marche ?

  • Dessin, dessin, dessin ! : tracez des graphiques, des diagrammes ou des illustrations pour donner vie aux concepts abstraits.
  • Utilisez des outils visuels : appliquez des logiciels comme GeoGebra pour manipuler des formes et explorer la géométrie de manière interactive.
  • Pensez en images : imaginez des triangles, des cercles ou des cubes lorsque vous travaillez sur des problèmes de géométrie ou d’algèbre.

Exemple pratique :

Vous apprenez les volumes ? Prenez un Rubik’s Cube ou une boîte, et comparez les formules avec les objets physiques. Vous comprendrez vite pourquoi V=a3 pour un cube : chaque face est une multiplication visuelle en deux dimensions et le volume est la multiplication des trois dimensions.

Après avoir navigué dans l’espace des formes, passons à un autre univers : celui des rythmes et des sons.

4. Intelligence musicale : faites des maths une mélodie

Cette intelligence se caractérise par une sensibilité aux rythmes, aux tonalités et aux timbres. Les personnes dotées d’une intelligence musicale élevée ont une capacité accrue à reconnaître, créer et reproduire des motifs musicaux.

Les maths et la musique ont une longue histoire d’amour. Si vous aimez les harmonies, les rythmes et les mélodies, vous pouvez transformer les maths en une partition.

Comment ça marche ?

  • Chantez vos formules : créez des chansons mnémotechniques pour mémoriser des concepts (par exemple, une mélodie pour réciter les carrés parfaits : 12=1, 22=4, 32=9,42=16… et ainsi de suite).
  • Apprenez les rythmes des maths : explorez les fractions en les comparant à des mesures musicales. Une mesure en 4 temps (4/4), c’est comme une division parfaite.
  • Découvrez les motifs musicaux dans les chiffres : Fibonacci, les suites arithmétiques, ou encore la relation entre \(\pi\) et les harmoniques musicales.

Exemple pratique :

Prenez la table de multiplication de 3. Associez chaque résultat à une note ou un battement dans un rythme répétitif. Par exemple :
– 3 x 1 = 3, tapez une fois sur la table.
– 3 x 2 = 6, tapez deux fois sur vos genoux.
– 3 x 3 = 9, ajoutez un claquement de mains.

Répétez ce cycle avec des variations rythmiques (par exemple, tapez plus vite ou créez un refrain avec un instrument improvisé). Cela transforme l’apprentissage en un exercice interactif et mélodique où le rythme devient un repère pour mémoriser les réponses. Ce type d’approche combine la répétition avec une stimulation sensorielle, ce qui ancre les concepts dans la mémoire tout en rendant l’expérience amusante et engageante. 😊

Si la musique est une façon de sentir les maths, que dire des mouvements corporels ? Voyons comment le corps peut également faire partie du jeu.

5. Intelligence corporelle-kinesthésique : bougez pour comprendre

L’intelligence corporelle-kinesthésique concerne la capacité à utiliser son corps pour exprimer des idées et des sentiments, ainsi que la facilité à utiliser ses mains pour créer ou transformer des choses. Les individus avec cette intelligence ont une bonne coordination œil-main et une dextérité fine.

Si vous apprenez mieux en bougeant ou en manipulant des objets, cette intelligence est votre point fort. Les maths peuvent devenir une danse ou une activité physique.

Les mouvements du corps permettent souvent des ancrages forts des apprentissages cognitifs.
Les mouvements du corps permettent souvent des ancrages forts des apprentissages cognitifs.

Comment ça marche ?

  • Rendez les maths tangibles : utilisez des objets comme des blocs, des jetons ou même des Legos pour visualiser des concepts.
  • Apprenez en bougeant : créez une chorégraphie dans laquelle chaque mouvement représente une étape d’une équation.
  • Jouez avec votre environnement : mesurez des distances réelles, pesez des objets ou faites des expériences pour comprendre les unités.

Exemple pratique :

Pour comprendre les angles, imaginez que vous êtes une aiguille d’horloge. Faites pivoter votre bras à différents degrés (90°, 180°, 360°) et visualisez comment ces mouvements s’appliquent aux horloges ou aux diagrammes.

Après avoir exploré l’énergie physique, plongeons dans l’univers des relations humaines avec l’intelligence interpersonnelle.

6. Intelligence interpersonnelle : apprenez avec les autres

Cette intelligence se manifeste par la capacité à comprendre et à interagir efficacement avec les autres. Les personnes dotées d’une forte intelligence interpersonnelle sont sensibles aux humeurs, aux sentiments et aux motivations des autres. Elles excellent dans la communication verbale et non verbale et peuvent voir les situations sous différents angles.

Vous êtes un(e) extraverti(e) dans l’âme ? Utilisez vos compétences sociales pour apprendre les maths en groupe.

Comment ça marche ?

  • Travaillez en groupe : discutez des problèmes mathématiques, expliquez vos solutions et apprenez des autres.
  • Utilisez les rôles : jouez à des jeux dans lesquels chacun incarne une partie de l’équation.
  • Aidez les autres : enseigner est souvent la meilleure façon de comprendre.

Exemple pratique :

Organisez une « battle mathématique » : un joueur pose un problème, et les autres doivent le résoudre dans un temps limité. Celui qui trouve la réponse explique sa méthode.

Bref ! Que vous soyez un linguiste passionné, un explorateur spatial ou un mélomane curieux, il y a toujours une manière d’apprendre les maths qui vous correspond. Les intelligences multiples ne sont pas des boîtes rigides, mais des clés pour ouvrir les portes de votre potentiel. Explorez, expérimentez et trouvez votre propre chemin vers les mathématiques. Après tout, il n’existe pas une seule bonne manière d’apprendre, mais une infinité de routes vers la compréhension. 😊

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !