Comment, vraiment, progresser en maths ?

Et si je vous disais que vous avez déjà tout ce qu’il faut pour réussir en maths ?

Non, ce n’est pas un énième discours de motivation pour la forme. Vous avez réellement en vous les capacités nécessaires pour comprendre, progresser et même exceller. Parfois, il suffit juste de changer de méthode. Apprendre les maths seul peut sembler intimidant au premier abord, mais c’est en réalité une aventure passionnante. Vous avancez à votre rythme, vous explorez ce qui vous intrigue, et surtout, vous apprenez à devenir autonome.

Comme le dit Jo Boaler, spécialiste reconnue des mathématiques et de l’éducation : « Les mathématiques ne sont pas une force mystique réservée à une élite. Elles sont un langage que chacun peut apprendre. » (En savoir plus sur Jo Boaler, en anglais)

Dans cet article, je vais vous montrer comment transformer cette aventure en un voyage organisé. Vous découvrirez des outils, des astuces et des étapes concrètes pour apprendre efficacement les maths, seul, sans stress. Que vous soyez un collégien, un lycéen ou même un adulte curieux, ces méthodes peuvent faire toute la différence. Alors, prêt à devenir votre propre prof de maths ?

Étape 1 : Comprendre ses forces et ses faiblesses

Vous n’êtes pas nul en maths. Sérieusement.
On a tous entendu un jour cette phrase : « Les maths, ce n’est pas fait pour moi« . Mais soyons honnêtes : c’est rarement vrai. Ce qui se cache derrière, c’est souvent un mélange de frustration, de craintes, d’a-priori et d’une mauvaise compréhension des bases. Benjamin Franklin, l’un des pères fondateurs des États-Unis d’Amérique, politicien, écrivain, philosophe, physicien, publiciste et imprimeur américain, disait : « Connaître ses lacunes est le premier pas vers la maîtrise. »
Reformulé en langage trivial d’aujourd’hui, ça donne : avant de te lancer dans l’apprentissage en solo, commence par savoir où tu en est.

Pourquoi c’est important ?

Apprendre efficacement, c’est comme préparer un voyage : vous devez savoir d’où vous partez pour choisir la bonne route. En maths, cela veut dire identifier vos forces (ce que vous maîtrisez déjà) et vos faiblesses (les notions qui vous échappent encore). Cette étape vous permet de ne pas perdre de temps à réviser ce que vous connaissez déjà ou, pire, à avancer en laissant des lacunes béantes derrière vous.

Comment s’y prendre ?

Voici une méthode en trois étapes pour faire un diagnostic simple et efficace :

1. Reprendre ses anciens devoirs ou contrôles
   Jetez un coup d’œil à vos notes, mais surtout aux erreurs commises. Est-ce que vous vous trompez sur les calculs ? Les notions théoriques ? L’interprétation des consignes ?
   Exemple : si vous avez souvent faux dans les exercices de proportionnalité, c’est probablement là qu’il faut creuser.
2. Faire un test de niveau rapide
   Il existe de nombreux tests en ligne pour évaluer vos compétences en maths. Des plateformes comme celle de Khan Academy permettent de cibler vos lacunes sur des chapitres spécifiques. C’est gratuit et je ne suis pas rémunérée pour les recommander.
   Exemple : En réalisant un test, vous découvrez que vous êtes à l’aise avec les additions fractionnaires mais que les équations du second degré restent un mystère total.
3. Créer une « carte mentale des maths »
   Prenez une feuille blanche et tracez un grand cercle. Notez-y les chapitres principaux (géométrie, algèbre, statistiques…). Autour de chaque chapitre, listez ce que vous pensez maîtriser et ce qui vous semble flou. Ce simple exercice visuel peut vous révéler des lacunes insoupçonnées.
   Exemple : Vous réalisez que si vous comprenez bien les formules de périmètre, les volumes restent flous.

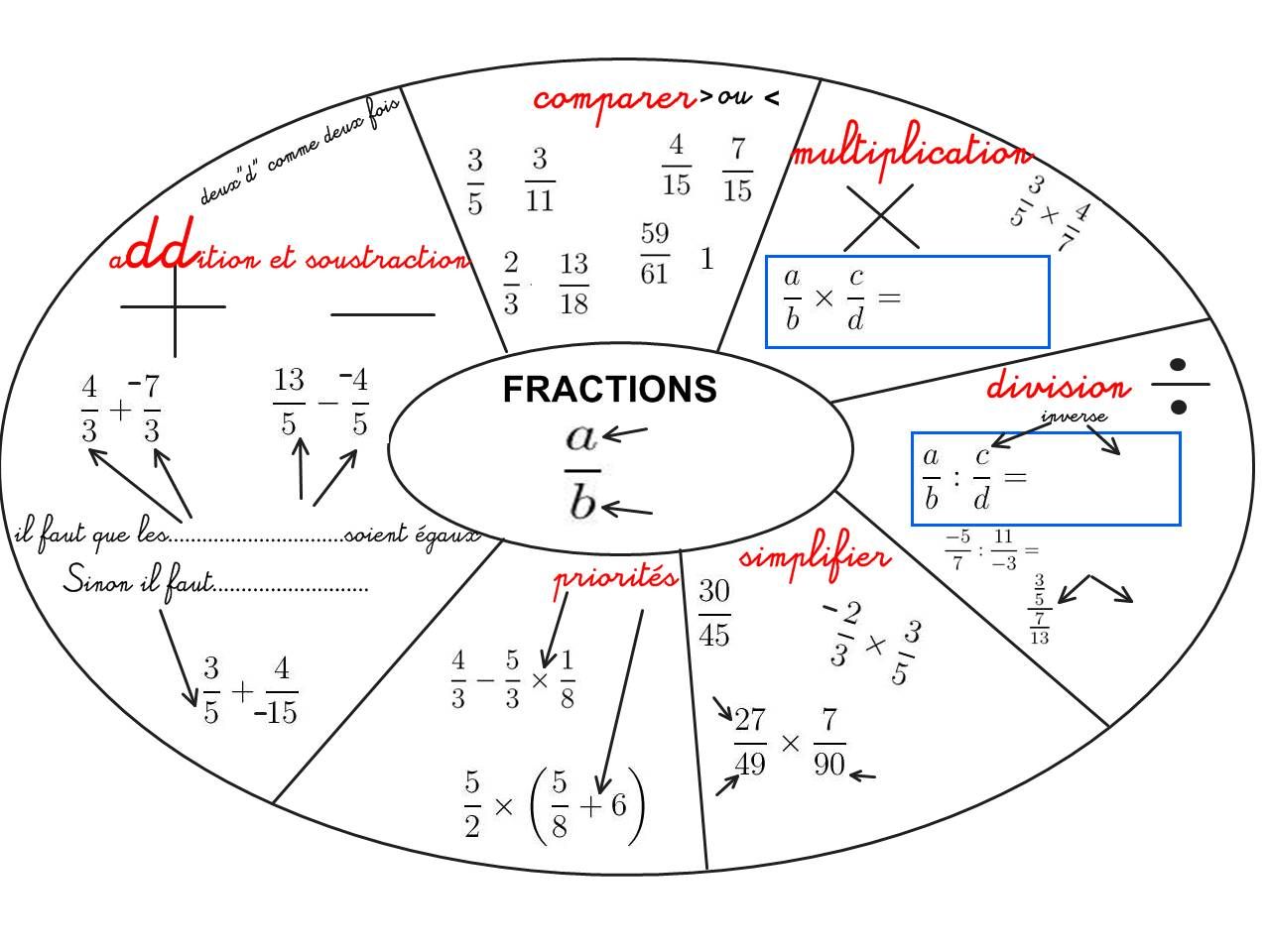
Faites donc comme Clara

Un jour, une de mes élèves, Clara, m’a confié qu’elle détestait les maths parce qu’elle n’arrivait jamais à se souvenir des formules. Alors, plutôt que de lui demander de les apprendre par cœur, je lui ai proposé de créer ses propres fiches, avec des dessins et des mots-clés qui lui parlaient. À sa grande surprise, elle s’est mise à retrouver d’elle-même les formules en les reliant aux situations qu’on avait travaillées. Ce n’était pas qu’elle manquait de mémoire, c’est qu’elle n’avait jamais essayé de comprendre les maths à sa manière.

Étape 2 : Fixer des objectifs clairs et mesurables

Apprendre les maths sans but précis, c’est un peu comme courir sans savoir où vous allez. Vous allez sûrement transpirer, mais finirez par tourner en rond. Le dégoût ! Fixer des objectifs, c’est donner une direction à vos efforts et mesurer vos progrès. Et franchement, rien ne motive plus que de constater qu’on avance !

C’est Antoine de Saint-Exupéry, le célèbrissime auteur du Petit Prince qui écrivait : « Un objectif sans plan n’est qu’un souhait« . Pour caricaturer, un plan, c’est ce qui fait la différence entre une velléité et une décision.

Pourquoi c’est important ?

En maths, les notions s’empilent comme des briques. Si une brique manque, tout s’effondre. Avoir des objectifs clairs vous aide à vous concentrer sur une brique à la fois, en construisant une base solide.

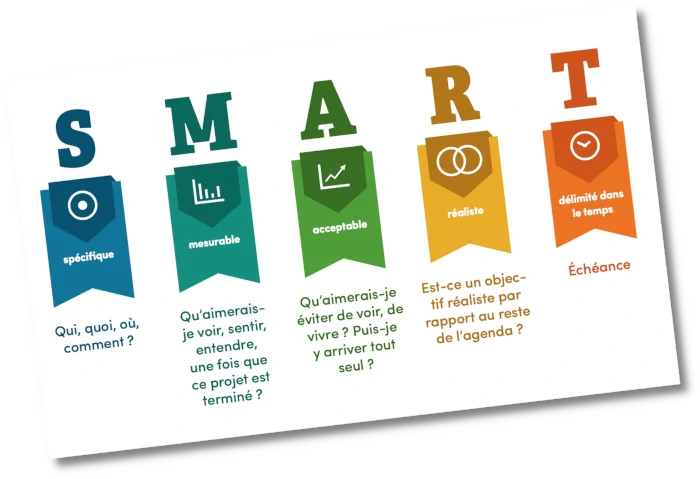
Un objectif bien défini doit être SMART :

• Spécifique : Pas de « Je vais mieux comprendre les maths », mais plutôt « Je vais apprendre à résoudre une équation du second degré. »
• Mesurable : Vous devez savoir si l’objectif est atteint. Par exemple, réussir 8 exercices sur 10.
• Atteignable : Fixez-vous des défis réalistes. Vouloir maîtriser tout le programme en une semaine, c’est le meilleur moyen de se décourager.
• Réaliste : Tenez compte de vos contraintes (temps, niveau actuel).
• Temporel : Donnez-vous une échéance claire. « Je veux maîtriser cette notion d’ici 10 jours. »

1. Partir de vos lacunes identifiées (voir Étape 1)
   Exemple : Si vous savez que les fractions vous posent problème, fixez un objectif précis comme « Comprendre l’addition et la soustraction de fractions d’ici la fin de la semaine. »
2. Découper vos objectifs en sous-objectifs
   Les maths, ça peut sembler une montagne, mais elle se gravit un pas à la fois. Plutôt que « Maîtriser les équations », commencez par « Comprendre les termes (inconnue, coefficient) » puis « Résoudre des équations simples ».
3. Associer chaque objectif à une ressource
   Si votre objectif est de comprendre les probabilités, cherchez des vidéos explicatives ou des exercices adaptés. Exemple : « Regarder la vidéo de Khan Academy sur les probabilités avant dimanche. »

Une méthode en pratique

Prenons l’exemple d’Emma, 15 ans. Elle veut comprendre les bases de la géométrie pour un contrôle. Voici son plan :
– Objectif principal : Comprendre les propriétés des triangles en une semaine.
– Objectifs intermédiaires :
1. Lundi : Apprendre les types de triangles (équilatéral, isocèle, etc.).
2. Mercredi : Comprendre les théorèmes associés (Pythagore, Thalès).
3. Vendredi : Réaliser 10 exercices corrigés.

Étape 3 : Trouver les bonnes ressources

Imaginez que vous essayez de résoudre un Rubik’s Cube sans tutoriel. Vous pourriez y arriver… mais probablement après de nombreuses heures et beaucoup de frustration. Maintenant, imaginez que quelqu’un vous explique les étapes, une par une. Le Cube vous semble tout de suite moins intimidant, non ? Apprendre les maths seul, c’est pareil : avoir les bonnes ressources, c’est comme avoir un guide qui vous montre le chemin.

Pourquoi c’est important ?

Les maths ne sont pas une matière qu’on peut apprendre en regardant passivement. Elles nécessitent des explications claires, des exemples bien choisis et des exercices progressifs. Une bonne ressource peut transformer une notion incompréhensible en quelque chose de presque évident. À l’inverse, une mauvaise ressource peut vous faire perdre un temps précieux, ou pire, vous décourager.

Les bons outils ne font pas tout,
mais ils rendent le chemin beaucoup plus agréable.

John Wooden, célèbre entraineur de basket-ball américain du siècle dernier

Les différents types de ressources

1. Les livres
   Les livres restent une base solide pour apprendre. Ils permettent de suivre une progression logique, souvent illustrée d’exemples et d’exercices.
   Exemples :
   • Les Maths pour les Nuls pour reprendre les bases de manière amusante.
   • Manuels scolaires de votre niveau : Les exercices progressifs sont souvent bien construits.
2. Les vidéos pédagogiques
   Rien de tel qu’une bonne vidéo pour visualiser une notion. Certaines chaînes YouTube expliquent les maths de façon simple et engageante.
   Exemples :
   • Yvan Monka : Idéal pour revoir les notions à votre rythme.
   • Micmaths : Pour explorer des concepts passionnants et amusants.
3. Les applications et sites interactifs
   Ces outils vous permettent de pratiquer avec des retours immédiats sur vos réponses.
   Exemples :
   • Mathway : Une aide pour résoudre des exercices étape par étape. Vous pouvez l’utiliser pour tricher en lui faisant faire vos devoirs ou lui faire décomposer toutes les étapes d’une résolution de problème pour comprendre et progresser. À vous de voir quels sont vos objectifs !
   • GeoGebra : Parfait pour la géométrie et les graphiques interactifs.
   • Brilliant : Une plateforme payante avec des défis mathématiques bien conçus.
4. Les forums et communautés en ligne
   Si vous êtes bloqué, il existe des forums dans lesquels vous pouvez poser des questions et recevoir de l’aide.
   Exemples :
   • Reddit MathHelp : Un espace collaboratif pour résoudre vos doutes.
   • Les-Mathematiques.net : Une communauté francophone très active (pour étudiants de premier cycle).

Comment choisir la bonne ressource ?

1. Identifiez ce qui vous aide à comprendre
   – Si vous êtes visuel : vidéos, schémas interactifs.
   – Si vous aimez lire et écrire : privilégiez les livres et les fiches.
2. Testez plusieurs outils
   Tout le monde n’apprend pas de la même façon. Essayez plusieurs ressources pour découvrir celles qui vous conviennent le mieux.
3. Alternez théorie et pratique
   Les maths ne se lisent pas : elles se pratiquent. Après avoir lu ou regardé une explication, passez immédiatement à des exercices pour appliquer ce que vous venez de comprendre.

Une méthode en pratique

Prenons l’exemple d’Anaïs, qui voulait comprendre les probabilités pour un contrôle :
– Elle a commencé par regarder une vidéo claire et simple sur YouTube pour revoir les bases.
– Ensuite, elle a fait une série d’exercices interactifs sur Khan Academy.
– Enfin, elle a utilisé un forum pour poser une question précise sur un problème qu’elle ne comprenait pas.

En combinant ces ressources, elle a non seulement compris, mais aussi gagné en confiance. Bref, soyez malins, soyez créatifs ! Allez chercher les méthodes qui vous conviennent.

Étape 4 : Créer une routine d’apprentissage

Apprendre les maths, c’est comme s’entraîner pour un sport : la régularité est plus importante que la quantité. Vous n’avez pas besoin de passer des heures chaque jour à travailler. Ce qu’il vous faut, c’est un rythme adapté, des séances courtes mais efficaces, et surtout une habitude bien ancrée.

La réussite, c’est l’application de petites habitudes chaque jour.

James Clear, auteur de Atomic Habits

Pourquoi c’est important ?

Les maths ne sont pas qu’une question de logique, c’est aussi une question de mémoire. Les notions doivent être pratiquées régulièrement pour passer de la compréhension à la maîtrise. Une routine structurée vous aide à rester motivé, à éviter la procrastination, et à faire des progrès constants, même avec un emploi du temps chargé.

Comment créer une routine efficace ?

1. Définissez un horaire fixe
   Choisissez un moment où vous êtes le plus concentré. Le matin, avant de commencer vos cours, ou en début de soirée sont souvent des créneaux efficaces.
   Exemple : « Chaque jour après le goûter, je consacre 20 minutes aux maths.« 
2. Fixez des objectifs pour chaque session
   Chaque séance doit avoir un but précis, comme « Faire trois exercices sur les fractions » ou « Regarder une vidéo sur les équations du second degré ». Cela vous évite de perdre du temps à décider quoi faire.
3. Alternez les activités
   Variez entre réviser une leçon, faire des exercices, et revoir vos erreurs pour ne pas vous ennuyer.
   Exemple : Une session type pourrait inclure 10 minutes pour revoir un théorème, 10 minutes d’exercices, et 5 minutes pour vérifier vos réponses.
4. Utilisez une méthode de gestion du temps
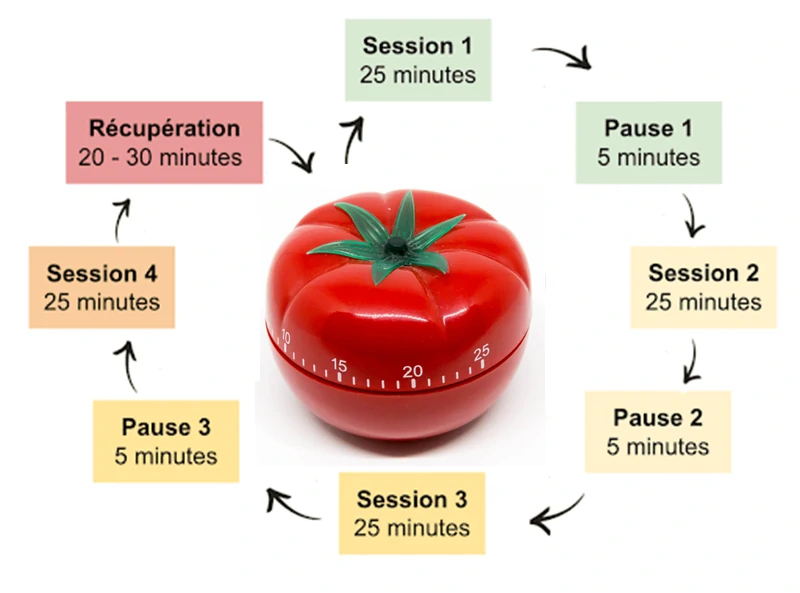
   Essayez la technique Pomodoro : travaillez pendant 25 minutes, puis prenez une pause de 5 minutes. Cela vous aide à rester concentré sans vous épuiser. Par exemple avec ToDoist.
5. Gardez une trace de vos progrès
   Notez les notions que vous avez maîtrisées et celles qui nécessitent encore du travail. Vous pouvez utiliser un tableau ou une application pour suivre votre progression.

Une soirée type pour les maths

Voici un exemple de routine simple mais efficace :
– Lundi :
– 17h00 : Réviser les bases des fractions (20 minutes).
– 17h30 : Faire 5 exercices corrigés.
– 17h50 : Vérifier les erreurs et noter ce qui n’est pas compris.
– Mardi :
– 17h00 : Regarder une vidéo sur les probabilités (15 minutes).
– 17h20 : Réaliser un exercice interactif en ligne (15 minutes).
– 17h40 : Écrire un résumé de ce qui a été appris.

Ce qu’il faut éviter

1. Les sessions interminables
   Travailler pendant deux heures d’affilée peut être contre-productif. Préférez plusieurs séances courtes et régulières.
2. Le multitâche
   Concentrez-vous sur une seule notion à la fois. Passer d’un sujet à l’autre peut être perturbant.
3. Les distractions
   Éloignez votre téléphone (sauf si vous utilisez une application), désactivez les notifications, et créez un espace calme pour travailler.

Étape 5 : Tester ses connaissances régulièrement

S’entraîner, c’est bien. Vérifier ses progrès, c’est encore mieux. En maths, rien ne remplace la pratique pour solidifier vos acquis et révéler les points à améliorer. Tester vos connaissances régulièrement, c’est comme un GPS pour votre apprentissage : vous savez où vous êtes et ce qu’il reste à parcourir.

Pourquoi c’est important ?

Quand vous faites des exercices ou des tests, vous ne faites pas que répéter des notions : vous les mettez à l’épreuve. Cela vous permet de :
1. Identifier les notions bien comprises et celles qui nécessitent encore du travail.
2. Ancrer durablement les concepts en passant de la théorie à la pratique.
3. Gagner en confiance, en voyant que vous progressez vraiment.

Comment bien tester ses connaissances ?

1. Faites des exercices variés
   Mélangez des exercices simples (pour consolider les bases) et des défis plus complexes (pour vous pousser à aller plus loin).
   Exemple : Réalisez des exercices progressifs dans votre manuel ou sur une plateforme comme Khan Academy.
2. Utilisez des annales ou des tests en ligne
   Les annales (anciens sujets de contrôle ou d’examen) sont une excellente ressource pour s’habituer aux formats d’évaluation et au niveau attendu.
   Exemple : Téléchargez des sujets de brevet ou de bac pour travailler en conditions réelles, comme sur le site de l’APMEP. Mais il y en a d’autres.
3. Corrigez vos erreurs
   Prenez le temps de comprendre pourquoi une réponse est incorrecte. Cela transforme une erreur en une opportunité d’apprentissage. « Apprendre, c’est faire des erreurs et les corriger« , disait Albert Einstein.
   Conseil : Tenez un journal de vos erreurs avec la solution correcte, pour y revenir plus tard.
4. Chronométrez-vous
   Les maths, ce n’est pas seulement trouver la bonne réponse, c’est aussi être capable de la trouver dans un temps donné. Entraînez-vous avec un chronomètre pour développer votre rapidité.
   Exemple : Résolvez 5 exercices en 15 minutes.
5. Apprenez à formuler des questions
   Tester vos connaissances ne se limite pas à répondre : posez-vous aussi des questions. « Pourquoi cette formule fonctionne-t-elle ? » ou « Dans quel cas ce théorème est-il applicable ? » Cela vous pousse à aller plus loin.

Une anecdote pour illustrer

Mathieu, élève en Terminale, avait des difficultés avec les probabilités. En travaillant des exercices variés, il s’est rendu compte qu’il confondait toujours deux formules. Après avoir noté ses erreurs et refait les exercices plusieurs fois, il a maîtrisé le sujet. Lors de son contrôle, il a même trouvé une solution astucieuse qu’il n’aurait jamais imaginée avant.

Ce qu’il faut éviter

1. Faire toujours les mêmes types d’exercices
   Répéter un exercice déjà maîtrisé ne vous apprend plus rien. Cherchez des variantes ou des problèmes plus complexes.
2. S’arrêter aux bonnes réponses
   Si une réponse est correcte, demandez-vous pourquoi elle l’est. Cela renforce votre compréhension.
3. Éviter les erreurs
   Les erreurs font partie de l’apprentissage. Ne les craignez pas, mais utilisez-les comme des points de repère pour progresser.

Conclusion : Une aventure accessible à tous

Apprendre seul les maths, c’est bien plus qu’une question de chiffres ou de théorèmes. C’est une compétence qui va bien au-delà des cours : c’est apprendre à résoudre des problèmes, à persévérer et à croire en votre capacité à comprendre ce qui semblait impossible hier.

Avec les bonnes méthodes, une routine adaptée et des ressources bien choisies, vous avez toutes les cartes en main pour réussir. Oui, il y aura des moments où vous aurez l’impression de stagner, mais souvenez-vous : chaque petit pas compte. Chaque erreur est une opportunité, chaque réussite une preuve que vous avancez. Et n’oubliez jamais ce qu’écrit Paul Lockart dans A Mathematician’s Lament, « Les maths, ce n’est pas trouver la bonne réponse, c’est apprendre à poser les bonnes questions.« 

Alors, lancez-vous. Faites le premier pas aujourd’hui. Et rappelez-vous : devenir autonome en maths, c’est aussi devenir plus fort dans la vie.

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !