Temps de lecture 7 minutes
Parlons aujourd’hui d’une méthode aussi efficace qu’élégante : la répétition espacée. Vous savez, cette technique qui consiste à réviser intelligemment au lieu de rester collé à son cahier jusqu’à ce que les formules vous dansent devant les yeux comme un écran de veille des années 2000.
Je vais vous montrer comment appliquer cette méthode à l’apprentissage des maths, que vous soyez collégien ou lycéen. Alors, c’est parti pour une plongée dans l’art de ne pas oublier ce qu’on vient d’apprendre !
La répétition espacée : qu’est-ce que c’est ?
Apprendre les mathématiques peut souvent ressembler à une montagne à gravir, avec des notions qui semblent disparaître dès qu’on tourne la page. La répétition espacée est une méthode idéale pour ancrer durablement ces connaissances et progresser de manière efficace. Voici comment elle fonctionne :
La répétition espacée, c’est un peu comme arroser une plante : vous ne videz pas tout votre arrosoir d’un coup (comprenez : réviser tout la veille du contrôle), mais vous donnez juste ce qu’il faut, au bon moment, pour que la plante (votre cerveau) puisse pousser tranquillement.
En clair, il s’agit de réviser les notions à des intervalles de plus en plus longs. Pourquoi ? Parce que c’est ainsi que fonctionne notre mémoire. La première fois que vous apprenez quelque chose, votre cerveau l’oublie rapidement. Mais si vous le revoyez avant que l’oubli soit complet, il le retient mieux. Et ainsi de suite, jusqu’à ce que cela devienne un souvenir durable. Merci Ebbinghaus et sa fameuse courbe de l’oubli !
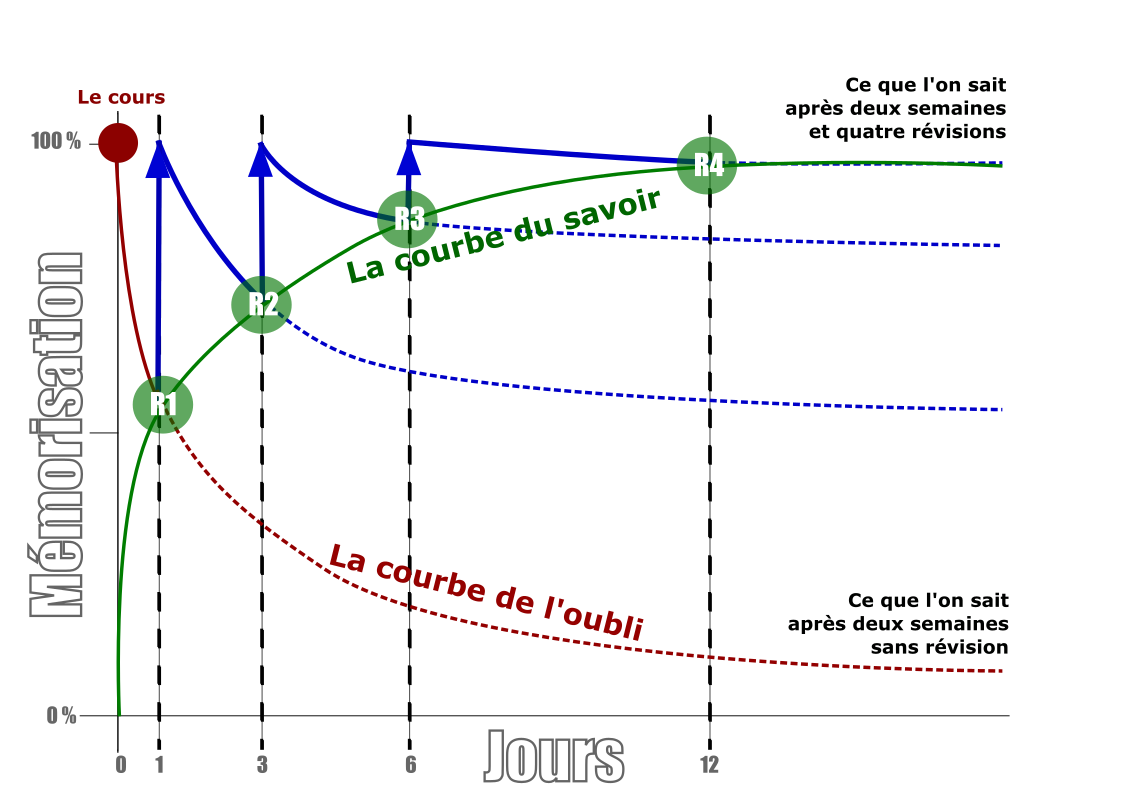
Faites une révision intégrale demain (R1) pour remettre votre mémoire au niveau de ce que vous saviez pendant le cours. Puis une autre dans trois jours (R2) et une autre dans 6 jours et peut-être même une dernière dans 12 jours.
Là, oui, vous aurez tout retenu et pour très longtemps. Votre mémoire aura suivi la courbe verte, celle de la mémorisation, du savoir.
En termes simples, c’est une technique qui vous aide à « muscler » votre mémoire. Et le meilleur, c’est que cette méthode fonctionne pour tout type d’apprentissage, mais elle est particulièrement puissante en maths.
Pourquoi la répétition espacée est-elle si efficace pour les maths ?
Les maths… Cette belle discipline où tout s’emboîte, mais où tout peut aussi s’effondrer si vous oubliez une petite formule au passage. La répétition espacée est particulièrement utile en maths parce que :
- C’est cumulatif : Les notions de maths s’accumulent comme des briques. Si vous avez oublié une brique de base (exemple : Pythagore), vous aurez du mal à bâtir un mur solide (exemple : trigonométrie).
- Les maths demandent de la pratique régulière : Il ne suffit pas de lire un théorème pour le comprendre. Il faut le manipuler, encore et encore.
- Cela aide à lutter contre la surcharge cognitive : Revisiter régulièrement les notions permet d’éviter d’“empiler” trop de nouvelles informations sans consolider les anciennes.
- Elle renforce la compréhension active : La répétition espacée, combinée à des exercices variés, aide à passer de la simple mémorisation à une compréhension approfondie. Vous ne vous contentez pas de réciter une formule, vous comprenez pourquoi elle fonctionne.
En somme, cette méthode s’adapte parfaitement à la nature logique et progressive des mathématiques.
Comment pratiquer la répétition espacée en maths ?
1. Identifiez ce qui doit être révisé
La première étape, c’est de savoir quoi réviser. Voici quelques pistes :
- Les formules : Aire d’un cercle, théorème de Thalès, trigonométrie, etc.
- Les démonstrations types : Exemple : Montrer que la somme des angles d’un triangle fait 180°.
- Les méthodes : Résoudre une équation du second degré, calculer une limite, tracer un graphique.
Pour chaque chapitre, faites une liste de ces éléments. Par exemple, dans un chapitre sur les fonctions, notez les notions essentielles : équations, variations, courbes et tangentes.
2. Organisez vos révisions
Adoptez un calendrier simple et progressif, basé sur les principes de la courbe de l’oubli : lorsque vous révisez une notion juste avant de l’oublier complètement, vous en renforcez la mémorisation de manière optimale. Ces intervalles progressifs permettent de ralentir le déclin naturel de la mémoire tout en consolidant les connaissances.
- Jour 1 : Vous apprenez la notion.
- Jour 2 : Vous la revoyez rapidement.
- Jour 4 : Vous la revalidez avec un exercice.
- Jour 8 : Vous la revoyez encore une fois.
- Jour 15 : Vous testez votre maîtrise.
C’est flexible : adaptez les intervalles à votre rythme et à la difficulté des notions.

3. Créez des fiches efficaces
Les fiches sont un outil puissant. Voici comment les organiser :
- Fiches pour les formules : Par exemple, une fiche pourrait contenir au recto la formule d’un cylindre (V = πr²h) accompagnée d’une explication claire de chaque terme, et au verso, un exemple chiffré : “Calculez le volume d’un cylindre de rayon 3 cm et de hauteur 5 cm”.
- Fiches pour les démonstrations : Listez les étapes clés d’une démonstration. Par exemple, pour le théorème de Thalès, incluez un schéma annoté sur le recto et les étapes de la preuve au verso.
- Fiches pour les erreurs courantes : Notez une erreur typique que vous faites, par exemple “Oublier de multiplier par le coefficient directeur”, et ajoutez au verso la réponse corrigée avec une explication de la solution.
4. Utilisez des outils numériques
Les applications comme Anki ou Quizlet sont parfaites pour appliquer la répétition espacée. Vous pouvez créer des cartes interactives :
- Question : Quelle est la dérivée de sin(x) ?
- Réponse : cos(x).
Ces outils permettent de suivre votre progression et de vous concentrer sur vos points faibles.
5. Adaptez les exercices aux révisions
Pour chaque révision, variez les types d’exercices :
- Au début : Des exercices simples pour fixer les bases.
- Progressivement : Des problèmes plus complexes pour renforcer votre maîtrise.
Exemple concret pour les collégiens et les lycéens
Prenons l’exemple des formules de trigonométrie (sinus, cosinus, tangente). Voici comment structurer vos révisions :
- Créez des fiches :
- Une fiche avec les valeurs exactes pour 0°, 30°, 45°, 60° et 90°.
- Une fiche avec les identités trigonométriques principales (cos²(x) + sin²(x) = 1).
- Apprenez par étapes :
- Jour 1 : Répétez les valeurs exactes à l’oral ou écrivez-les.
- Jour 4 : Faites un exercice simple où vous devez utiliser ces valeurs.
- Jour 8 : Essayez un exercice plus complexe où vous combinez plusieurs notions.
- Testez-vous :
- Créez un quiz rapide sur ces formules.
- Réalisez des exercices corrigés pour vérifier votre compréhension.
Les erreurs à éviter
Parce que, oui, même la meilleure méthode peut être mal appliquée :
- Ne pas respecter les intervalles : Si vous laissez passer trop de temps entre deux révisions, vous oublierez tout. Inversement, répéter trop souvent peut être contre-productif.
- Se contenter de lire : La révision passive (“Je lis ma fiche”) est bien moins efficace que la révision active (“Je résous un exercice”).
- Vouloir tout faire d’un coup : Priorisez les notions essentielles.
Compléments et approfondissements
Associer la répétition espacée à d’autres techniques
- Pratique active : Combinez la répétition avec des exercices variés.
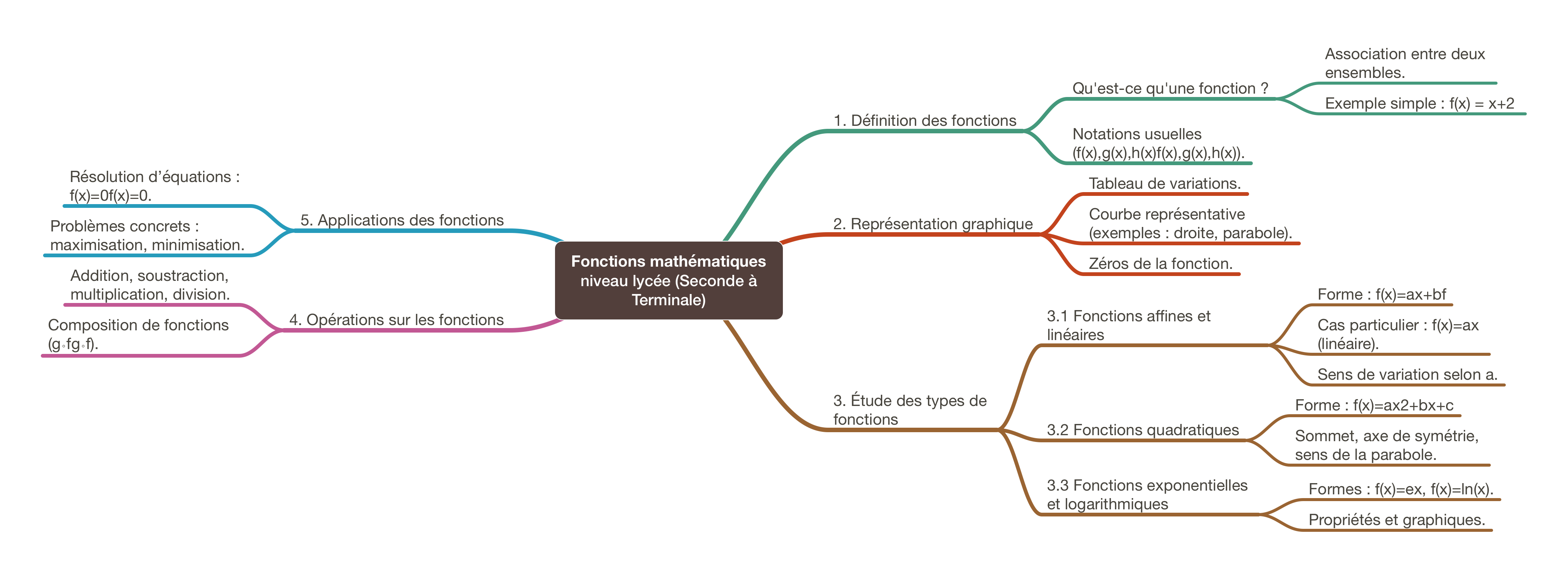
- Mind maps : Créez des cartes mentales pour visualiser les liens entre différentes notions.
- Gamification : Transformez vos révisions en jeu (score, défis).
Un plan sur l’année scolaire
- Avant les contrôles : Revoir les notions à intervalles réguliers.
- Pendant les vacances : Consolider les bases et anticiper les prochains chapitres.
- Préparation aux examens : Reprendre systématiquement les notions clés depuis le début de l’année.
>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !
Un dernier mot
La répétition espacée, c’est un peu comme l’entretien d’une voiture : il faut y aller régulièrement pour éviter les pannes (ou les trous de mémoire en plein contrôle !). Alors, prenez le temps de structurer vos révisions, soyez patients et, surtout, amusez-vous à constater vos progrès. Vous verrez, les maths deviendront moins intimidantes et bien plus accessibles.
Et si vous avez des questions ou des retours d’expérience, partagez-les dans les commentaires. Je suis là pour vous aider à développer vos super-pouvoirs mathématiques !
Quelques ressources gratuites
Pour vous donner un coup de main et pour vous montrer qu’on peut facilement s’organiser pour être plus efficace dans ses révisions, je vous ai préparé trois petits modèles qui pourraient vous être utiles. Vous êtes libres de les télécharger, de vous en inspirer, de les modifier mais surtout… de vous en servir !


