Les nombres premiers sont les stars des mathématiques. Comme les acteurs principaux d’un film, ils peuvent sembler simples à première vue, mais leur importance dépasse l’écran. Définis comme des nombres entiers divisibles uniquement par eux-mêmes et par 1, ils sont les fondations de notre système numérique. On les utilise, souvent sans le savoir, dans tout ce qui touche à la cryptographie, les codes secrets et même la théorie musicale.
Mais revenons à leurs bases. Prenez un nombre comme 126 : vous pouvez le décomposer en \(2 \times 3 \times 3 \times 7\) , où chaque facteur est un nombre premier. Cette propriété, appelée factorisation unique, est si fondamentale qu’elle est au cœur de nombreux systèmes mathématiques modernes. Sans ces briques de base, l’édifice des entiers s’effondrerait.
Ce qui fascine les mathématiciens, c’est leur répartition. Si vous regardez la liste des premiers nombres premiers – 2, 3, 5, 7, 11, etc. –, elle semble aléatoire. Entre deux d’entre eux, vous trouverez parfois un grand vide, et parfois des successions presque collées. Pourquoi ? Nul ne le sait vraiment. Cécile Dartyge, chercheuse en arithmétique, explique : « On sait qu’il existe des intervalles arbitrairement grands sans aucun nombre premier, mais leur répartition reste un mystère ». Ce caractère imprévisible en fait une source inépuisable d’interrogations.
Certains les comparent aux étoiles : apparemment dispersées au hasard, leurs positions suivent pourtant des règles fondamentales que nous essayons de comprendre depuis des siècles. Une analogie que la science adore, car, comme pour les étoiles, l’infini est leur seule limite.
Mais si ces mystères vous intriguent, attendez de découvrir jusqu’où la technologie nous emmène pour explorer ces géants numériques.
La Chasse aux Géants : Quand les Maths rencontrent la Technologie
Le plus grand nombre premier connu à ce jour possède… 41 millions de chiffres. Imaginez-le : il faudrait remplir 10 423 pages A4 pour l’écrire entièrement. Ce mastodonte a été découvert grâce au projet collaboratif GIMPS, qui utilise la puissance des ordinateurs pour détecter de nouveaux premiers de Mersenne. Ces nombres prennent une forme particulière, \(2^p – 1\), où \(p\)est aussi un nombre premier. Leur structure simplifie les tests de primalité.
Mais pourquoi chasser ces colosses ? C’est à la fois un défi intellectuel et une aventure collective. Luke Durant, l’un des participants au projet, raconte : « C’est un peu comme chercher une aiguille dans une botte de foin. Mais quand on la trouve, c’est une victoire partagée par toute une communauté ». GIMPS montre comment des amateurs et des chercheurs peuvent collaborer grâce aux outils numériques, rendant les mathématiques accessibles à tous.
Les nombres premiers géants ne sont toutefois qu’un petit échantillon parmi une infinité encore inexplorée. Une quête sans fin ? Peut-être. Mais chaque nouvelle découverte éclaire un peu plus les mystères des nombres premiers. Par ailleurs, ces découvertes ne sont pas qu’académiques : elles influencent directement la sécurité de vos données.
Cryptographie et Nombres Premiers : Votre Bouclier Numérique
Depuis les années 1970, les nombres premiers ont révolutionné le monde de la cryptographie. C’est grâce à eux que vos données bancaires restent confidentielles. Tout repose sur une idée simple : multiplier deux grands nombres premiers est facile, mais retrouver ces nombres à partir du produit est incroyablement difficile.
Prenons un exemple. Si je vous dis que 34 833 059 est le produit de deux nombres premiers, combien de temps vous faudrait-il pour retrouver 4 421 et 7 879 ? Une éternité ! Maintenant, imaginez des nombres de 300 chiffres. Même les ordinateurs les plus puissants mettraient des centaines d’années à résoudre ce casse-tête.
Le chiffrement RSA, qui repose sur ce principe, est devenu un standard pour sécuriser les communications. Plus la puissance des ordinateurs augmente, plus il est nécessaire d’utiliser des nombres premiers gigantesques pour maintenir la sécurité. Ainsi, des géants comme \(2^{136279841} – 1\)— c’est le tout dernier nombre premier qui vient d’être découvert — pourraient un jour protéger vos transactions.
Anne-Gwénaëlle de Roton, mathématicienne, précise : « L’étude des nombres premiers nous permet aussi d’évaluer la robustesse des systèmes de chiffrement. C’est une course contre la montre entre les chercheurs en sécurité et ceux qui tentent de casser ces codes. » Les nombres premiers, loin d’être de simples curiosités mathématiques, sont ainsi vos gardiens invisibles.
Pourtant, leur rôle en cryptographie n’est qu’un chapitre de leur histoire.
Mystères et Révélations : L’Hypothèse de Riemann et Au-Delà
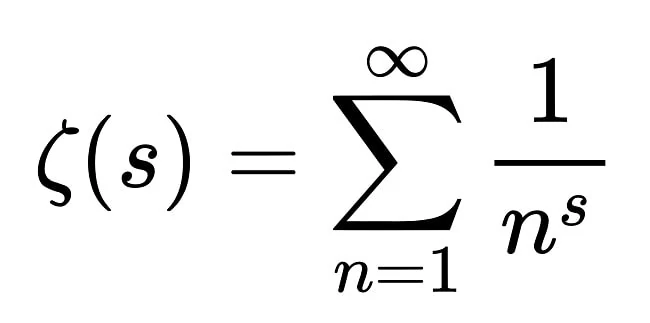
Au cœur des recherches actuelles se trouve l’hypothèse de Riemann, une conjecture qui, si elle était prouvée, révolutionnerait notre compréhension des nombres premiers. Formulée en 1859, elle reste l’un des « problèmes du millénaire » non résolus, avec une récompense d’un million de dollars pour quiconque la démontrera. Cette hypothèse cherche à expliquer la répartition des nombres premiers, offrant une clé pour percer leur mystère.
Récemment, des avancées ont été réalisées par des chercheurs comme Larry Guth (MIT) et James Maynard (Oxford). Leurs travaux, bien que non encore validés, permettent d’affiner notre compréhension de la répartition des nombres premiers. Ces progrès rappellent que les mathématiques sont une science vivante, où chaque découverte ouvre de nouvelles portes.
Saviez-vous que… ?
- Les nombres premiers sont partout : Ils interviennent même dans des domaines inattendus comme la musique, où ils définissent des intervalles harmoniques.
- Un défi mondial : Le plus grand nombre premier de Mersenne a été découvert grâce à un réseau mondial d’ordinateurs personnels. Vous pourriez contribuer en rejoignant GIMPS !
- Un problème ancien : Euclide a démontré l’infinité des nombres premiers… il y a plus de 2 300 ans.
Une Fenêtre sur l’Infini
Les nombres premiers sont bien plus que des abstractions mathématiques ; ils incarnent l’essence de l’exploration humaine. À travers leur étude, nous plongeons dans des questions fondamentales sur l’ordre et le chaos, le fini et l’infini. Ils protègent vos données, inspirent les chercheurs et nous rappellent que, même dans un monde de certitudes numériques, il reste de vastes territoires à découvrir.
>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !


