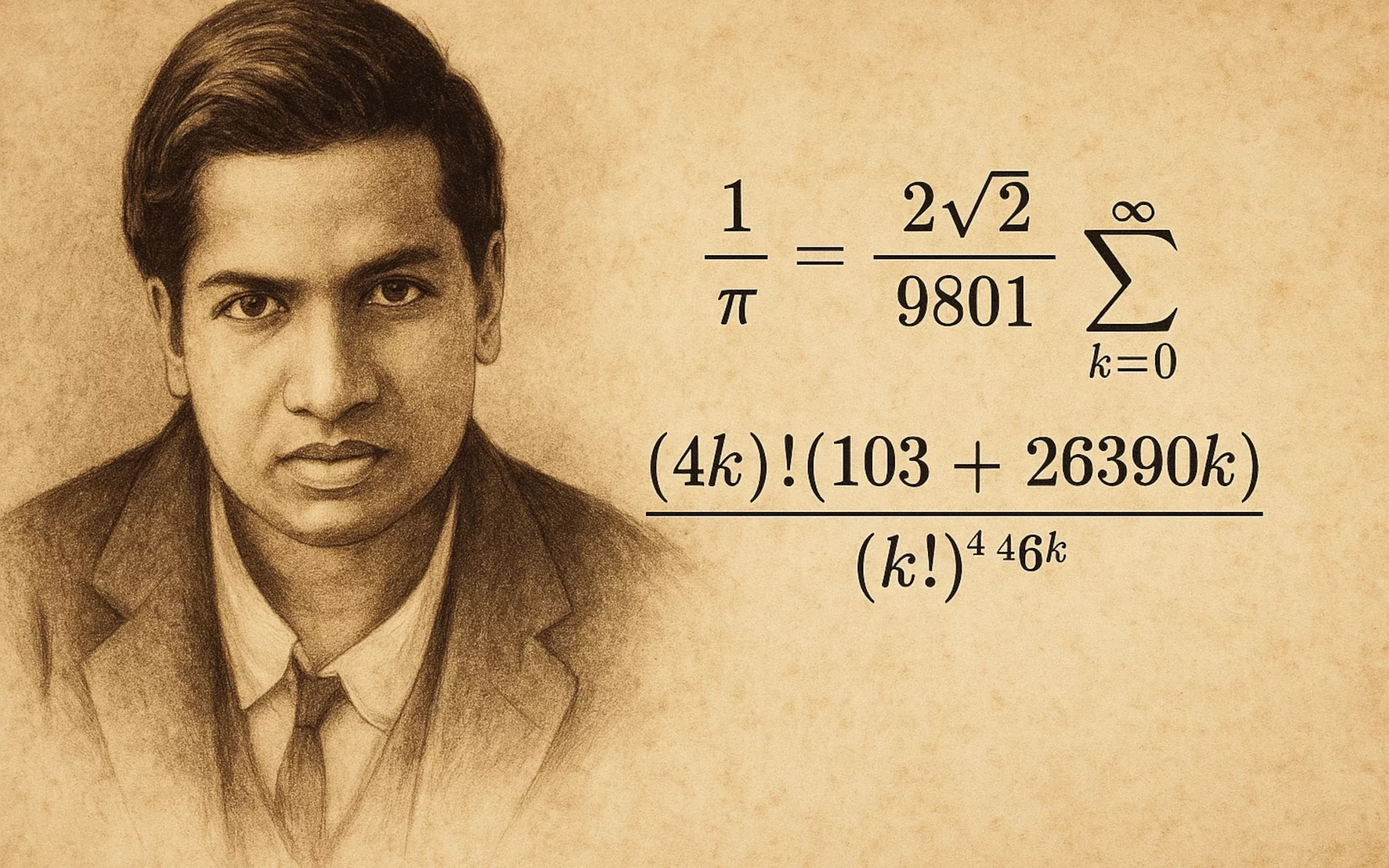Ramanujan : un génie mathématique hors du commun

temps de lecture 7 minutes

Il y a des noms qui, même s’ils restent méconnus du grand public, brillent d’une lumière presque mystique dans le ciel des mathématiques. Srinivasa Ramanujan est de ceux-là. Sa vie ressemble à un roman. Son travail, à une musique que seuls quelques rares élus peuvent entièrement déchiffrer. Mais son histoire, elle, parle à tout le monde. Et surtout à celles et ceux qui se demandent comment progresser en maths quand on n’a pas toutes les cartes en main.

Aujourd’hui, je t’emmène à la rencontre de ce génie autodidacte, né sans manuel, sans mentor, sans méthode… mais pas sans passion. Et si tu penses que les maths sont un domaine réservé aux crânes d’élite, Ramanujan pourrait bien te faire changer d’avis.

Une vie hors du commun

Ramanujan naît en 1887 à Erode, dans le sud de l’Inde, dans une famille modeste de brahmanes. Son père est comptable dans un magasin de tissus, sa mère chante des chants religieux dans un temple. Rien ne le prédestine à devenir mathématicien.

Et pourtant, très jeune, il se passionne pour les chiffres. À dix ans, il dévore tout ce qui lui tombe sous la main. Mais il n’a accès qu’à un seul livre vraiment marquant : le « Synopsis of Elementary Results in Pure and Applied Mathematics » de G.S. Carr, un manuel britannique aride, bourré de formules sans explication. Ramanujan le mémorise presque entier. Il le recopie. Il le digère. Puis, il se met à inventer ses propres théorèmes. Beaucoup. Des centaines. Puis des milliers.

Mais l’école ne suit pas. Obsédé par les maths, il n’étudie plus rien d’autre. Il est brillant en arithmétique, mais coule dans les autres matières. Alors, il rate ses examens et quitte plusieurs fois le système scolaire. Et, pendant des années, il vit dans la pauvreté, errant d’un emploi à l’autre, notant ses trouvailles sur des carnets qu’il garde précieusement.

C’est en 1913 qu’il décide d’écrire à plusieurs professeurs anglais, en joignant quelques-unes de ses « formules ». La plupart l’ignorent. Mais un homme, Godfrey Harold Hardy, mathématicien de Cambridge, s’arrête, relit… et comprend qu’il est face à un génie. « Certains de ces résultats doivent être vrais, car personne n’aurait l’imagination de les inventer », écrit-il.

J’ai découvert en Ramanujan un mathématicien d’un tout autre ordre que moi. Je n’ai jamais rencontré d’esprit mathématique aussi créatif. Il était un feu.

(adapté d’écrits de Hardy)

Hardy le fait venir en Angleterre. Ramanujan, qui n’a jamais quitté son Tamil Nadu natal, débarque à Cambridge au début de la Première Guerre mondiale. Il y travaillera pendant cinq ans, produisant une quantité énorme de recherches, avant de rentrer en Inde, malade et affaibli. Il meurt en 1920, à seulement 32 ans.

Une intuition mystique au service des mathématiques

Ramanujan ne travaillait pas comme les autres mathématiciens de son temps. Il n’avait pas de méthode formelle, pas de formation classique, et pourtant, il produisait des formules d’une profondeur et d’une justesse stupéfiantes. Il affirmait que ses idées lui étaient inspirées en rêve par la déesse Namagiri, qui lui apparaissait et lui montrait les formules comme des révélations. Cette approche quasi mystique ne l’empêchait pas d’être d’une rigueur redoutable dans l’intuition.

Hardy dira de lui : « Il était un mathématicien de premier plan, mais il pensait comme aucun autre mathématicien avant lui. »

Son œuvre touche à des domaines à la fois fondamentaux et très techniques :

• Les fonctions modulaires, objets mathématiques liés à la théorie des nombres, qui apparaissent aujourd’hui dans la physique théorique et les formes modulaires.
• La théorie des partitions d’entiers : combien de façons peut-on décomposer un nombre en une somme d’entiers ? Ramanujan a découvert des résultats prodigieux sur ces questions.
• Les séries infinies : il a réussi à donner des formules d’une précision incroyable pour calculer des constantes comme π.

Par exemple, cette formule qui a émerveillé les mathématiciens :

\[
\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum_{k=0}^\infty
\frac{(4k)! (1103 + 26390k)}{(k!)^4 \, 396^{4k}}
\]

Elle permet de calculer π avec une vitesse de convergence fulgurante. Aujourd’hui encore, elle est utilisée dans des algorithmes de calcul ultra-précis.

Mais ce n’est pas tout : Ramanujan a aussi défini ce qu’on appelle aujourd’hui les « Ramanujan primes », les « Ramanujan theta functions », ou encore la fameuse « Ramanujan tau function »… Beaucoup de ses notes, non publiées de son vivant, ont révélé des perles longtemps après sa mort.

Ce qu’on peut apprendre de lui pour progresser en maths

1. Ne pas attendre de tout comprendre pour explorer

Ramanujan ne connaissait pas les théories modernes, les langages formels, les notations rigoureuses. Il a pourtant plongé. Parce qu’il était porté par la curiosité et la joie de découvrir. Il faut parfois oser se lancer même quand on ne « maîtrise pas encore ».

2. Faire confiance à son intuition… mais la tester ensuite

Ramanujan produisait beaucoup de résultats par intuition. Certains étaient incorrects ou approximatifs. Mais beaucoup étaient justes, et incroyablement puissants. Ce qu’on en tire ? L’intuition est un moteur. Elle doit ensuite être nourrie, corrigée, éclairée par la vérification.

3. Chercher la beauté

Oui, la beauté. Ramanujan disait : « Une équation n’a pas de sens pour moi si elle n’exprime pas une pensée de Dieu. » Cette quête de l’harmonie, du mystère et de l’élégance peut être un véritable moteur d’étude. Les maths ne sont pas que des règles. Ce sont des paysages à contempler.

4. Accepter les erreurs comme partie du chemin

Il a été critiqué, incompris, parfois ridiculisé. Il a fait des erreurs. Mais il a continué. Parce qu’il savait que se tromper fait partie du processus d’apprentissage.

5. Oser sortir des sentiers battus

Ramanujan ne suivait pas les chemins balisés. Il proposait des idées sans cadre, sans contexte. Cela l’a rendu difficile à comprendre… mais c’est aussi ce qui a fait sa richesse. En maths, poser une question un peu folle peut ouvrir des portes.

6. Persévérer malgré les obstacles

Il a raté ses examens, été ignoré, rejeté. Pourtant, il n’a jamais arrêté de croire que ce qu’il faisait avait du sens. Travailler les maths, c’est souvent douter. On peut avancer, même quand on n’a pas toutes les clés.

7. Trouver des figures inspirantes

Hardy, pour Ramanujan, a été plus qu’un mentor : un passeur. Parfois, il suffit de croiser quelqu’un qui croit en nous pour débloquer tout un monde. Cherche autour de toi ceux qui encouragent ta curiosité.

>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !

À chacun sa façon de briller

Tu n’es pas Ramanujan. Personne ne l’est. Mais tu peux, comme lui, suivre ton fil, creuser une idée, faire confiance à ta curiosité. Tu peux, comme lui, poser des questions, chercher de la beauté, rêver avec les maths. Et tu peux surtout te rappeler que les génies ne sont pas toujours dans les bancs des meilleures écoles. Parfois, ils sont dans une chambre modeste, un carnet à la main et une étoile dans la tête.

Alors, à toi de jouer. Les maths ne sont pas un monde fermé. C’est un monde à explorer. Il n’attend que toi.