Pourquoi les enfants apprennent-ils sans comprendre l’intérêt d’apprendre ?
Temps de lecture 8 minutes
Aujourd’hui, je m’écarte un peu des sentiers battus pour une petite expérience de pensée qui m’a semblé aussi amusante qu’éclairante. Attachez vos ceintures, on monte d’un cran dans l’abstraction, mais promis, on garde les pieds sur terre à la découverte du paradoxe de l’apprentissage des maths !
Imaginez un instant qu’une intelligence artificielle ultraperformante — disons Leïa, pour lui donner un nom — se retrouve soudainement incarnée dans le corps d’une ado de 12 ans. Et disons aussi que cette IA conserverait ses formidables méthodologies d’apprentissage, sa capacité à structurer l’information, à établir des connexions, mais aucune de ses connaissances préalables. Comment s’y prendrait-elle pour apprendre les mathématiques en partant de zéro, comme un enfant humain ?

C’est la question un peu folle que je me suis posée lors d’une soirée insomniaque. Et, franchement, mes élucubrations m’ont offert une perspective fascinante sur l’apprentissage humain et ses paradoxes.
Le plan d’apprentissage idéal de notre « IA-enfant »
Leïa, contrairement à beaucoup de mes chers élèves (je vous aime quand même !), aborderait probablement l’apprentissage des mathématiques avec une stratégie bien définie :
Elle commencerait par cultiver une curiosité naturelle envers les patterns et relations numériques dans son environnement quotidien. Les formes dans la nature, les proportions dans l’architecture, les rythmes dans la musique… Dans sa boulimie cognitive, tout deviendrait terrain d’exploration mathématique !
Leïa privilégierait la compréhension conceptuelle plutôt que la mémorisation. Exit les formules apprises par cœur sans comprendre d’où elles viennent ! Notre IA-ado chercherait systématiquement le « pourquoi » derrière chaque règle, construisant des modèles mentaux solides avant de passer à la suite.
Elle utiliserait diverses approches d’apprentissage : manipulation d’objets concrets, visualisations, application des concepts à des situations pratiques… La diversité serait son maître-mot. (J’approuve cette approche à 200 % !)
Notre IA s’efforcerait d’établir des connexions entre différents domaines mathématiques, cherchant à voir comment l’algèbre, la géométrie et l’arithmétique s’informent mutuellement. Elle construirait une véritable toile de connaissances interconnectées plutôt qu’une série de compartiments séparés.
Face aux difficultés, Leïa développerait une attitude de « croissance » en voyant les erreurs comme des opportunités d’apprentissage. « Tiens, j’ai fait une erreur dans cette équation… Formidable ! Qu’est-ce que cela m’apprend ? » (Oui, on sait, pas facile d’avoir cette réaction quand on vient de rater un contrôle…)
Elle rechercherait activement des mentors et des ressources adaptées à son style d’apprentissage, et essaierait d’enseigner ce qu’elle apprend à d’autres pour renforcer sa compréhension. Car, comme le disait un certain Albert : « Si vous ne pouvez pas l’expliquer simplement, vous ne l’avez pas assez bien compris. »
Bref, Leïa serait cette élève parfaite que tous les profs de maths rêvent d’avoir dans leur classe. (Arrête de rêver, Sophie, et reviens parmi nous !)
La réalité des jeunes humains
Mais voilà, les vrais enfants humains ne fonctionnent pas tout à fait comme notre IA théorique. Et pour cause !
Plusieurs facteurs entrent en jeu :
Le développement cérébral joue un rôle crucial. Les enfants ont des capacités d’abstraction limitées qui évoluent progressivement avec l’âge. Certains concepts mathématiques requièrent des fonctions cognitives qui ne sont tout simplement pas encore « installées » dans leur cerveau. C’est comme vouloir faire tourner un logiciel sophistiqué sur un ordinateur qui n’a pas encore téléchargé tous ses composants !
Les facteurs émotionnels ont un impact considérable. L’anxiété mathématique est réelle et souvent transmise par l’entourage. Combien de fois ai-je entendu un parent dire devant son enfant : « Moi aussi j’étais nul(le) en maths à ton âge ? Ces croyances limitantes deviennent des prophéties autoréalisatrices et moi, je rage en silence derrière mon grand sourire.
Les méthodes d’enseignement traditionnelles privilégient parfois la mémorisation et les procédures au détriment de la compréhension conceptuelle. « Apprenez cette formule, on verra plus tard pourquoi elle fonctionne » — une approche qui fonctionne pour certains, mais qui en laisse beaucoup d’autres sur le carreau.
Le contexte social influence aussi fortement l’apprentissage. L’attitude des parents et des enseignants envers les mathématiques façonne celle des enfants. Dans certains milieux, les mathématiques sont présentées comme difficiles, ennuyeuses ou peu pertinentes pour « la vraie vie ».
Et n’oublions pas les contraintes systémiques : classes surchargées, programmes rigides, évaluations standardisées… Ces contraintes limitent souvent les approches personnalisées et créatives que notre IA-enfant adopterait naturellement.
Le grand paradoxe de l’apprentissage
Et c’est là que j’arrive au cœur de ma réflexion, à ce paradoxe fascinant qui a émergé de ma petite expérience de pensée :
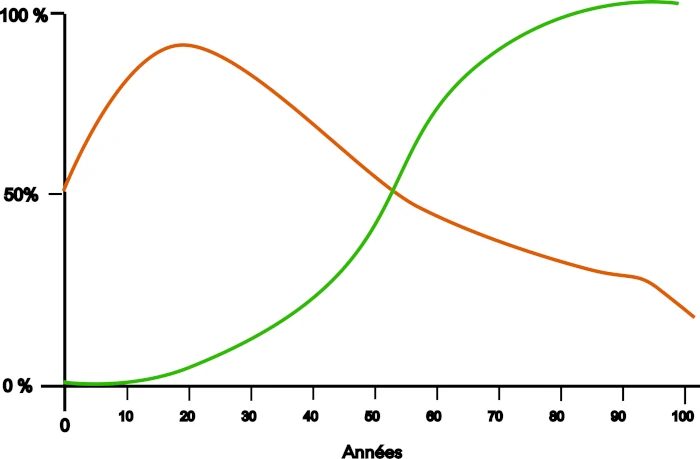
Le meilleur moment biologique pour apprendre est souvent le pire moment psychologique pour comprendre la valeur de cet apprentissage.
N’est-ce pas délicieusement absurde ? La nature humaine nous a dotés de cerveaux incroyablement plastiques et réceptifs durant l’enfance et l’adolescence – c’est la période où nous pouvons apprendre le plus facilement et où les connaissances se « gravent » le mieux. Mais c’est aussi la période où nous sommes le moins équipés pour comprendre pourquoi nous devrions apprendre ces choses !
Je vis souvent cette scène qui se répète dans mes cours particuliers :
- L’élève : « Mais Madame, à quoi ça sert les vecteurs dans la vraie vie ? »
- Moi : « Eh bien, ils sont fondamentaux en physique, en informatique, en économie… »
- L’élève (les yeux déjà ailleurs) : « Oui, mais moi, je veux être TikTokeur… »
Le supermarché de la connaissance
L’ironie est presque poétique : nous apprenons sans comprendre pourquoi, pour plus tard comprendre sans avoir à réapprendre. C’est comme si la nature avait programmé notre développement pour que nous accumulions des ressources dont nous ne percevrons la valeur que des années plus tard.
Cela me rappelle mon compagnon qui s’efforçait d’expliquer à son fils l’intérêt de travailler quand il était en classe de seconde et qu’il n’en avait tout simplement pas envie : « Imagine que le lycée est un supermarché de la connaissance, disait-il. Tu as un immense caddie et tu peux prendre tout ce qui te tombe sous la main. Imagine le festin que tu feras toute ta vie avec ça ! »
Je dois reconnaitre que la parabole était sympa, mais le fiston n’en avait pas grand-chose à faire. Amasser des provisions pour l’avenir n’a guère de sens quand on a 15 ans et qu’on ne sait même pas ce qu’on va faire dans 10 minutes.
Et quand enfin, adultes, nous saisissons pleinement l’importance de ces connaissances, notre capacité d’apprentissage naturel a déjà commencé à diminuer. Combien d’adultes se disent : « Si seulement j’avais prêté plus attention en cours de maths… » ? (Je peux vous le confirmer : beaucoup !)
Que faire de ce paradoxe ?
Alors, comment travailler avec ce paradoxe plutôt que contre lui ? Voici quelques pistes que j’explore dans mes approches pédagogiques :
- Créer des ponts entre l’abstrait et le concret. Montrer aux jeunes comment les concepts mathématiques s’appliquent à des domaines qui les passionnent déjà. Les jeux vidéo sont pleins de mathématiques. TikTok aussi (si, si, les algorithmes de recommandation, ce sont des maths !).
- Accepter que la motivation extrinsèque a sa place. Oui, bien sûr, dans l’idéal, j’aimerais que tous mes élèves apprennent pour le pur plaisir de comprendre. Mais, en attendant que cette motivation intrinsèque se développe, il n’y a pas de honte à utiliser des encouragements externes.
- Cultiver l’attitude de « croissance » chez les jeunes. Leur montrer que l’intelligence n’est pas fixe et que le cerveau est comme un muscle qui se développe avec l’effort.
- Être honnête sur la valeur différée. Parfois, il faut simplement reconnaître auprès des jeunes : « Oui, tu ne vois peut-être pas l’utilité immédiate de ce concept, et c’est normal. Fais-moi confiance, ça te servira plus tard. »
- Adapter notre enseignement aux capacités développementales des enfants. Certains concepts mathématiques nécessitent des fonctions cognitives qui se développent à des âges précis – respectons ces étapes !
Apprendre à apprendre
Ma petite expérience de pensée avec Leïa me rappelle une vérité fondamentale : au-delà des mathématiques elles-mêmes, c’est la capacité à apprendre qui est peut-être la compétence la plus précieuse que je puisse transmettre.
Si notre IA-enfant imaginaire possède un avantage sur les humains, c’est bien celui-là : elle sait comment apprendre efficacement. Et c’est sûrement là que réside la clé pour résoudre notre paradoxe : en enseignant aux jeunes non seulement des connaissances mathématiques, mais aussi des méthodes d’apprentissage qui leur serviront toute leur vie.
Comme je le dis souvent à mes élèves : « Mon but n’est pas que tu réussisses juste ton prochain contrôle, mais que tu n’aies plus besoin de moi après. »
>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !
Et vous, qu’en pensez-vous ? Ce paradoxe vous parle-t-il ? Avez-vous vécu cette étrange dissonance entre disposition d’apprentissage et compréhension de sa valeur ? Partagez vos réflexions en commentaires !
En attendant, continuez à explorer le monde fascinant des mathématiques avec curiosité et bienveillance envers vous-mêmes. Et n’oubliez pas : même les IA imaginaires trouveraient que les maths humaines sont un sacré défi !




