Temps de lecture 6 minutes.
Vous avez sûrement déjà remarqué qu’en musique, tout est question de rythme, de mesures et de proportions. Derrière chaque note jouée, il y a une structure mathématique bien définie. Que vous soyez musicien ou matheux, ces deux mondes sont plus proches qu’on ne le pense. Si vous avez suivi quelques cours sur ce sujet, vous savez déjà que les fréquences, les harmoniques et les fractions rythmiques sont au cœur de la musique. Mais comment cela peut-il réellement influencer notre compréhension des maths ? Comment peut-on tirer parti de la musique pour mieux comprendre les mathématiques et inversement ? Plongeons ensemble dans cet univers fascinant entre maths et musique.
Maths et musique : une relation ancestrale
Depuis l’Antiquité, musique et mathématiques sont liées. Pythagore, l’un des premiers à explorer cette connexion, a découvert que les intervalles musicaux reposent sur des ratios mathématiques précis. Une corde vibrante coupée en deux produit la même note mais une octave plus haute. Les accords consonants reposent sur des proportions simples comme 3/2 (quinte) ou 5/4 (tierce majeure). Cette découverte a influencé toute la théorie musicale occidentale.
Au fil des siècles, cette relation n’a cessé d’être étudiée. Des compositeurs comme Bach ont utilisé des structures mathématiques complexes dans leurs œuvres, exploitant la symétrie, les inversions et même la suite de Fibonacci. Certains estiment même que les œuvres de Bach sont des puzzles mathématiques sophistiqués, où chaque note et chaque motif obéissent à des règles précises.
À l’époque classique, d’autres compositeurs comme Mozart et Beethoven ont utilisé des principes mathématiques pour structurer leurs œuvres. Par exemple, Mozart intégrait parfois la suite de Fibonacci dans la répartition de ses accords, créant ainsi une harmonie naturelle et équilibrée. Beethoven, quant à lui, jouait avec la symétrie et les proportions dorées pour construire ses sonates.
Avec l’essor de la technologie, la relation entre mathématiques et musique s’est encore approfondie. Le XXe siècle a vu émerger des compositeurs comme Iannis Xenakis, qui a combiné algèbre, probabilités et musique pour créer des compositions basées sur des modèles mathématiques avancés. Ses pièces utilisent des principes de la théorie des ensembles et des fractales pour générer des structures sonores innovantes.
Aujourd’hui, la musique algorithmique permet de composer des œuvres entières à partir de formules mathématiques. Grâce aux ordinateurs, des algorithmes génèrent automatiquement des compositions en appliquant des règles mathématiques strictes. C’est le cas dans certains genres expérimentaux et dans la musique assistée par intelligence artificielle.
Un peu de lecture
Si vous souhaitez approfondir ce sujet, voici deux ouvrages de référence :

Gödel, Escher, Bach : Les Brins d’une Guirlande Éternelle de Douglas Hofstadter, qui explore les parallèles entre musique, mathématiques et logique.

Music: A Mathematical Offering de David Benson, qui examine en détail les principes mathématiques sous-jacents à la musique.
D’autres livres, comme The Geometry of Music de Dmitri Tymoczko, analysent également comment les principes géométriques influencent la musique et la composition. Enfin, les travaux du physicien et musicologue Ernst Guillemin sur l’acoustique musicale offrent une perspective scientifique approfondie sur les liens entre mathématiques et perception musicale.
Les structures mathématiques cachées dans la musique
Le rythme et les fractions : une question de division
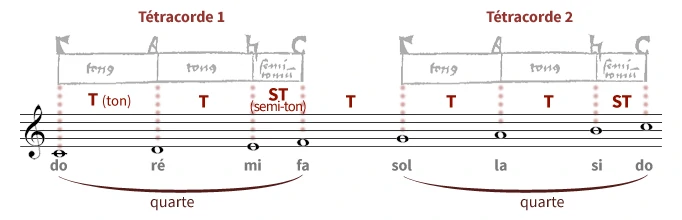
Dans une mesure en 4/4 (très courante en musique), chaque temps est une fraction d’un tout. Une noire dure 1/4 de mesure, une blanche 1/2 et ainsi de suite. Si vous avez déjà travaillé sur les fractions en maths, vous avez sans doute remarqué la similarité avec la division et les proportions. Comprendre le solfège, c’est manipuler des fractions sans même y penser.
Les compositeurs, consciemment ou non, organisent les rythmes de manière mathématique, jouant avec les valeurs de notes pour créer des motifs cohérents et équilibrés. Certains morceaux utilisent des signatures rythmiques inhabituelles (5/4, 7/8) qui exigent une approche plus fine des fractions et de la division.
Un exemple célèbre est le célébrissime morceau Take Five de Dave Brubeck, qui joue sur une mesure en 5/4, inhabituelle mais captivante. L’utilisation de ces signatures rythmiques joue directement avec notre perception mathématique du temps et de la régularité.
Les harmoniques et les nombres : la physique du son
Outre le rythme, la musique repose aussi sur la fréquence des sons. Un son musical est une onde, et ses harmoniques sont définies par des lois mathématiques strictes. Les notes d’un accord bien réglé suivent une progression harmonique qui peut être décrite à l’aide de séries mathématiques. L’accord parfait majeur, par exemple, se base sur des relations numériques simples entre les fréquences des notes.
Ce lien entre mathématiques et musique est encore plus frappant dans les instruments à cordes. La longueur des cordes vibrantes détermine la fréquence du son, et des équations précises permettent de calculer les fréquences des notes selon leur longueur, leur section et leur tension.
Un autre exemple marquant est celui de Stravinsky, qui utilisait des transformations géométriques pour créer des motifs musicaux. Il jouait avec les symétries et les permutations pour créer de nouvelles sonorités.
La musique pour mieux comprendre les maths
Une stimulation cérébrale efficace
Pratiquer un instrument mobilise simultanément plusieurs compétences : coordination, logique, anticipation. Ces facultés améliorent naturellement la capacité à résoudre des problèmes mathématiques, qui nécessitent également logique et structuration.
Jouer un instrument ou chanter impose aussi une rigueur rythmique et une gestion du temps qui rappellent la gestion des équations en mathématiques. Une partition, tout comme un problème mathématique, doit être décomposée en éléments plus simples avant d’être exécutée.
Études et résultats scientifiques
Des études ont montré que les élèves pratiquant un instrument développent une meilleure habileté à raisonner en mathématiques. Une recherche menée en Californie a démontré que des enfants suivant des cours de piano étaient plus performants en résolution de problèmes que ceux n’ayant pas d’apprentissage musical.
D’autres travaux ont mis en évidence que l’écoute régulière de musique pouvait renforcer certaines capacités cognitives. Notamment la mémoire de travail et la reconnaissance des schémas. Ces compétences sont essentielles en mathématiques, particulièrement pour la résolution de problèmes complexes.
Comment intégrer la musique dans les révisions ?
- Utiliser des morceaux instrumentaux comme support de concentration.
- Transformer des formules mathématiques en mélodies pour les retenir plus facilement.
- Analyser les motifs musicaux sous un prisme mathématique : Identifier les cycles, les symétries et les progressions.
- Créer des exercices de calcul basés sur la musique : Par exemple, calculer les durées cumulées de plusieurs notes ou prédire la fréquence d’une note selon sa longueur de corde.
- Expérimenter les transformations géométriques sur des mélodies : Étudier comment les transpositions et les inversions d’une séquence musicale se rapprochent des symétries et transformations en mathématiques.
>>> N’oubliez pas de vous abonner à ma lettre d’information et de demander votre ebook gratuit !
Une synergie à exploiter
La musique et les maths sont deux disciplines étroitement liées. En les combinant, on améliore non seulement la compréhension théorique des concepts, mais aussi la créativité et la capacité d’analyse.
Que vous soyez passionné de musique ou féru de maths, il existe de nombreuses façons d’explorer cette connexion. Alors, pourquoi ne pas utiliser votre prochaine séance de musique pour réviser vos maths d’une manière différente ? 🎶
Pour aller plus loin dans la découverte de cette fascinante relation entre la musique et les maths, je vous invite à consulter le site mathetmusique.fr.




